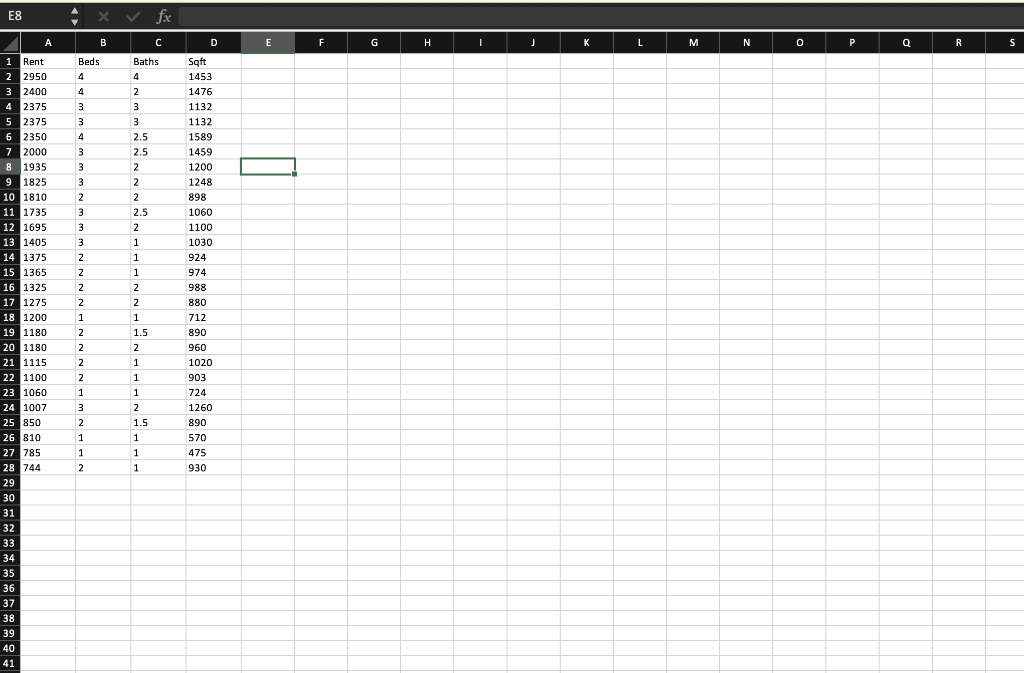
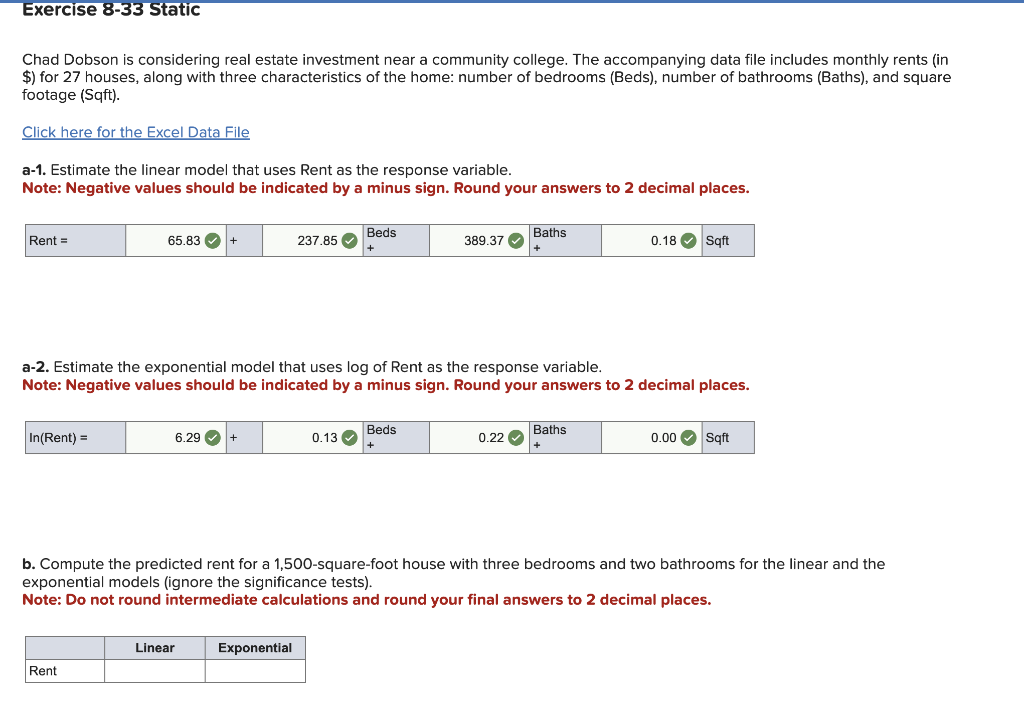
E8 A B fx C Baths Sqft 1 Rent Beds 2 2950 4 4 1453 3 2400 4 2 1476 4 2375 3 3 1132 5 2375 3 3 1132 6 2350 4 2.5 1589 7 2000 3 2.5 1459 8 1935 3 2 1200 9 1825 3 2 1248 10 1810 2 2 898 11 1735 3 2.5 1060 12 1695 3 2 1100 13 1405 3 1 1030 14 1375 2 1 924 15 1365 2 1 974 16 1325 2 2 988 17 1275 2 2 880 18 1200 1 1 712 19 1180 2 1.5 890 20 1180 2 2 960 21 1115 2 1 1020 22 1100 2 1 903 23 1060 1 1 724 24 1007 3 2 1260 25 850 2 1.5 890 26 810 1 1 570 27 785 1 1 475 28 744 2 1 930 29 30 31 32 33 34 35 36 37 38 39 40 41 D E F G H J K L M N P Q R S Exercise 8-33 Static Chad Dobson is considering real estate investment near a community college. The accompanying data file includes monthly rents (in $) for 27 houses, along with three characteristics of the home: number of bedrooms (Beds), number of bathrooms (Baths), and square footage (Sqft). Click here for the Excel Data File a-1. Estimate the linear model that uses Rent as the response variable. Note: Negative values should be indicated by a minus sign. Round your answers to 2 decimal places. Rent= 65.83 237.85 Beds + Baths 389.37 0.18 Sqft a-2. Estimate the exponential model that uses log of Rent as the response variable. Note: Negative values should be indicated by a minus sign. Round your answers to 2 decimal places. In(Rent) = 6.29 0.13 Beds + Baths 0.22 0.00 Sqft b. Compute the predicted rent for a 1,500-square-foot house with three bedrooms and two bathrooms for the linear and the exponential models (ignore the significance tests). Note: Do not round intermediate calculations and round your final answers to 2 decimal places. Linear Rent Exponential