Each order can have multiple products, the relation can make with binary variables.

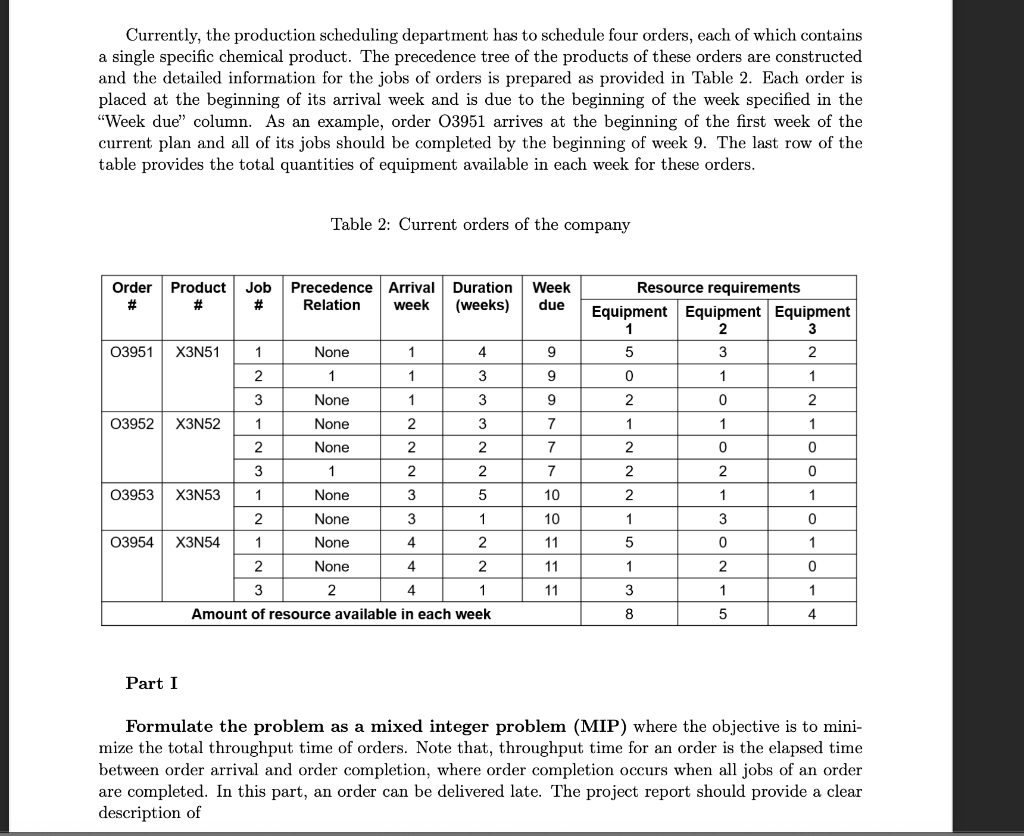
In this project, you will work on a production scheduling problem of a chemical company that produces batches of chemical products on demand. Equipment1, Equipment2, and Equipment3 are the three primary types of equipment used in the production facility. There are currently 17 equipment, where 8 of them are of type Equipment1, 5 of them are of type Equipment2, and the remaining 4 are of type Equipment3. Demand from customers arrives in the form of orders. Orders consist of batches of one, two, or three custom chemical products, and they must be supplied at the exact time of order due date. For each product in an order, a sort of special pilot plant consisting of specific quantities of these equipment should be constructed. Some products may need to be processed by more than one of these pilot plants. In such cases, one or more batches of intermediate products are produced for further processing. Typically, the equipment on hand is not sufficient to meet the current demand. The production scheduling department of the company prepares the production schedule in a weekly manner. Once a new order is received, the industrial engineer in charge of production scheduling prepares a precedence tree for each product of the corresponding order. Through the precedence tree, each product of the order is divided into a number of jobs, where each job requires the use of a specific pilot plant (that includes specific quantities of equipment) for a specific duration. Currently, the production scheduling department has to schedule four orders, each of which contains a single specific chemical product. The precedence tree of the products of these orders are constructed and the detailed information for the jobs of orders is prepared as provided in Table 2. Each order is placed at the beginning of its arrival week and is due to the beginning of the week specified in the "Week due" column. As an example, order O3951 arrives at the beginning of the first week of the current plan and all of its jobs should be completed by the beginning of week 9 . The last row of the table provides the total quantities of equipment available in each week for these orders. Table 2: Current orders of the company Part I Formulate the problem as a mixed integer problem (MIP) where the objective is to minimize the total throughput time of orders. Note that, throughput time for an order is the elapsed time between order arrival and order completion, where order completion occurs when all jobs of an order are completed. In this part, an order can be delivered late. The project report should provide a clear description of Formulate the problem as a mixed integer problem (MIP) where the objective is to minimize the total throughput time of orders. Note that, throughput time for an order is the elapsed time between order arrival and order completion, where order completion occurs when all jobs of an order are completed. In this part, an order can be delivered late. The project report should provide a clear description of - the decision variables, 2 - the objective function, and - constraints After constructing the main model, analyze the alternative objective functions. Alternative objectives are given as: - Minimizing makespan - Minimizing total lateness - Minimizing maximum lateness Describe how the mathematical model you constructed should be updated for each alternative