eBookeBook

Problem 13-01

please show me how this was solved using excel. I don't understand the pv as % of price.

Calculate the Macaulay duration of a 9%, $1,000 par bond that matures in three years if the bond's YTM is 12% and interest is paid semiannually.

Calculate this bond's modified duration. Do not round intermediate calculations. Round your answer to two decimal places.

1. years

2. Assuming the bond's YTM goes from 12% to 11.0%, calculate an estimate of the price change. Do not round intermediate calculations. Round your answer to three decimal places. Use a minus sign to enter negative value, if any.

   %

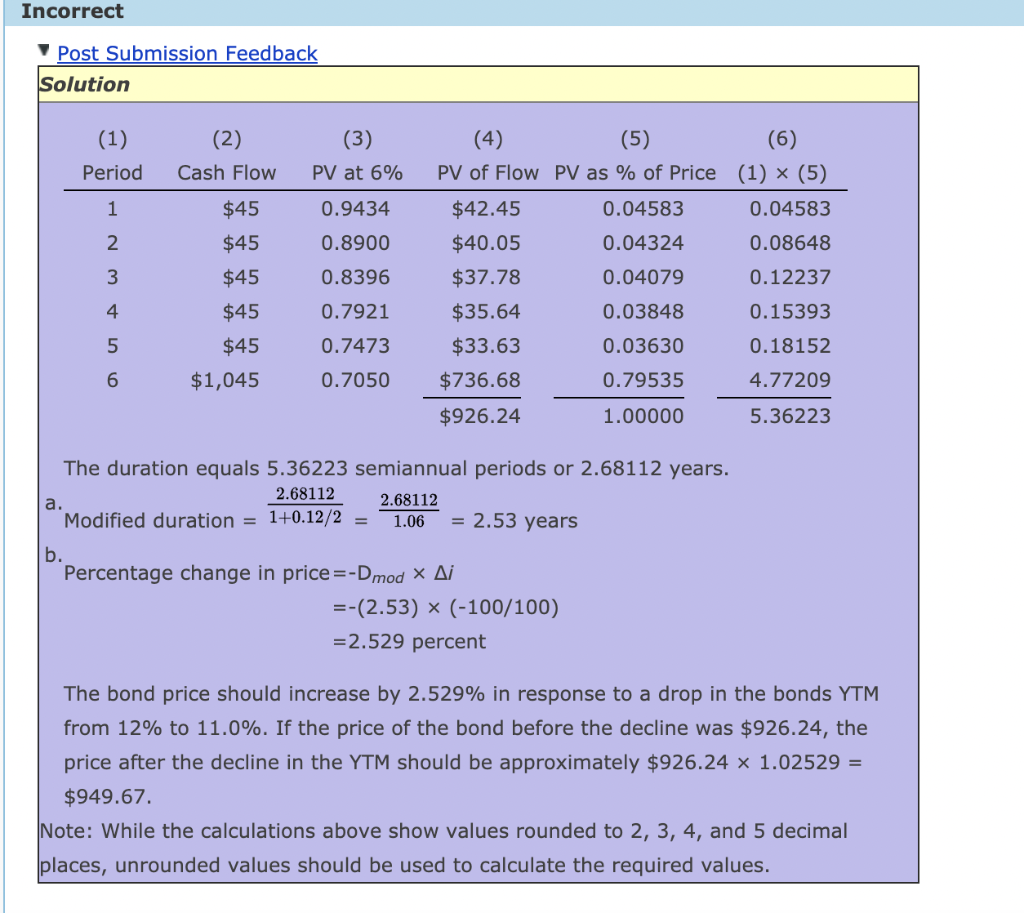
Incorrect Post Submission Feedback Solution (2) (1) Period (3) PV at 6% Cash Flow 1 $45 0.9434 0.8900 2 $45 3 0.8396 (4) (5) (6) PV of Flow PV as % of Price (1) x (5) $42.45 0.04583 0.04583 $40.05 0.04324 0.08648 $37.78 0.04079 0.12237 $35.64 0.03848 0.15393 $33.63 0.03630 0.18152 $736.68 0.79535 4.77209 $926.24 1.00000 5.36223 $45 $45 $45 4 0.7921 5 0.7473 6 $1,045 0.7050 The duration equals 5.36223 semiannual periods or 2.68112 years. 2.68112 2.68112 Modified duration = 1+0.12/2 = 1.06 = 2.53 years a. b. Percentage change in price =-Dmod X Ai =-(2.53) * (-100/100) =2.529 percent The bond price should increase by 2.529% in response to a drop in the bonds YTM from 12% to 11.0%. If the price of the bond before the decline was $926.24, the price after the decline in the YTM should be approximately $926.24 x 1.02529 = $949.67. Note: While the calculations above show values rounded to 2, 3, 4, and 5 decimal places, unrounded values should be used to calculate the required values