Edit following code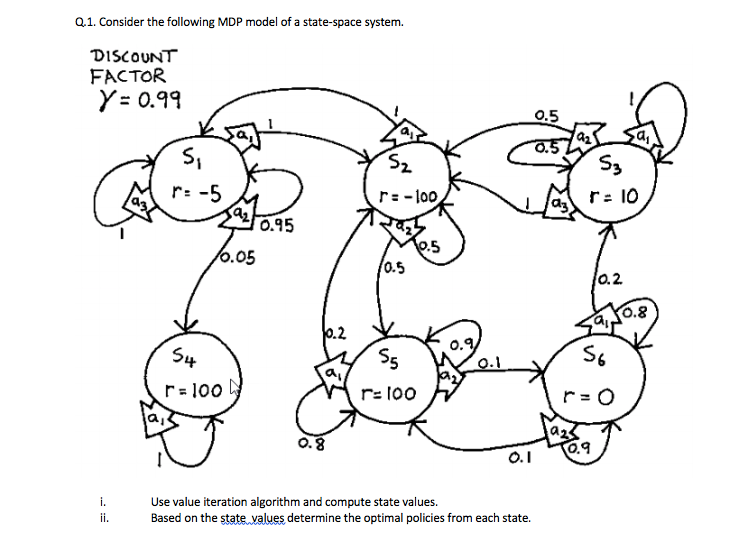

# -*- coding: utf-8 -*- """ Created on Sat May 16 13:24:11 2020

@author: ACAN """

# The value iteration algorithm import numpy as np

""" A SIMPLE EXAMPLE Suppose a 3x4 Environment that has an obstacle at location (2,2). Action probabilities: P(intended Direction)=0.8, P(perpendicular Directions)=0.1. When the agent hits a wall, it bounces back to its current cell. """

R=np.array([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])

# Rows correspond to Actions and Columns # correspond to states E=np.array([[-1,-1, -1, -1, -1, -1], [-1, 0, 0, 0, +1, -1], [-1, 0, -1, 0, -1, -1], [-1, 0, 0, 0, 0, -1], [-1,-1, -1, -1, -1, -1]]) V0=np.array([[0., 0., 0., +1.], [0., 0., 0., -1.], [0., 0., 0., 0.]]) # Initial Values V=V0 Rows=5 Cols=6 Goal_Pos=[(0,3)] Value_in_GoalPos=+1

# Actions: Go to North, South, East, West probilistically such that # moving towards the intended direction is with probability 0.7 and moving # along any other three direction is with probability 0.1.

epsilon=0.00000000000001 # Termination threshold value gamma=0.9 # Discount factor gamma

iter_count=0 # Number of iterations until convergence

is_done=False while not is_done: iter_count += 1 Vprev = np.array(V) # Vprev keeps previous V values for i in range(Rows): for j in range(Cols): if E[i,j]==0: # For each free state if not(E[i-1,j] == -1): U_West=R[i-1,j-1]+gamma*Vprev[i-2,j-1] else: U_West=R[i-1,j-1]+gamma*Vprev[i-1,j-1] if not(E[i+1,j] == -1): U_East=R[i-1,j-1]+gamma*Vprev[i,j-1] else: U_East=R[i-1,j-1]+gamma*Vprev[i-1,j-1] if not(E[i,j-1] == -1): U_South=R[i-1,j-1]+gamma*Vprev[i-1,j-2] else: U_South=R[i-1,j-1]+gamma*Vprev[i-1,j-1] if not(E[i,j+1] == -1): U_North=R[i-1,j-1]+gamma*Vprev[i-1,j] else: U_North=R[i-1,j-1]+gamma*Vprev[i-1,j-1] North_Move=0.7*U_North+0.1*U_West+0.1*U_East+0.1*U_South South_Move=0.7*U_South+0.1*U_West+0.1*U_East+0.1*U_North West_Move=0.7*U_West+0.1*U_South+0.1*U_North+0.1*U_East East_Move=0.7*U_East+0.1*U_South+0.1*U_North+0.1*U_West if (i-1,j-1) not in Goal_Pos: # V[i-1,j-1]=max([North_Move,South_Move,West_Move,East_Move]) V[i-1,j-1]=0.25*(North_Move+South_Move+West_Move+East_Move) if sum(sum((Vprev-V)**2))

print(' ')

V_Strategy=[[]] for i in range(Rows-2) : for j in range(Cols-2): if i==0: if j==0: NBList=[(i,j+1),(i+1,j)] elif j==Cols-3: NBList=[(i,j-1),(i+1,j)] else: NBList=[(i,j-1),(i,j+1),(i+1,j)] elif i==Rows-3: if j==0: NBList=[(i,j+1),(i-1,j)] elif j==Cols-3: NBList=[(i,j-1),(i-1,j)] else: NBList=[(i,j-1),(i,j+1),(i-1,j)] elif j==0: NBList=[(i-1,j),(i+1,j),(i,j+1)] elif j==Cols-3: NBList=[(i-1,j),(i+1,j),(i,j-1)] else: NBList=[(i,j-1),(i,j+1),(i-1,j),(i+1,j)] Max=V[NBList[0][0],NBList[0][1]] Max_Tuple=NBList[0] for k in range(1,len(NBList)): if V[NBList[k][0],NBList[k][1]] > Max: Max=V[NBList[k][0],NBList[k][1]] Max_Tuple=NBList[k] if not (E[Max_Tuple[0]+1,Max_Tuple[1]+1] == -1): if Max_Tuple[0]==i: if Max_Tuple[1]>j: V_Strategy[i].append([u'\u2192']) else: V_Strategy[i].append([u'\u2190']) elif Max_Tuple[1]==j: if Max_Tuple[0] > i: V_Strategy[i].append([u'\u2193']) else: V_Strategy[i].append([u'\u2191']) else: V_Strategy[i].append([" "]) V_Strategy.append([])

for i in range(Rows-2) : for j in range(Cols-2): print(V_Strategy[i][j][0],end='') print()

Q.1. Consider the following MDP model of a state-space system. DISCOUNT FACTOR Y= 0.99 0.5 0.5 Si r:-5 S2 S3 03 r: -100 dy r: 10 0.95 0.5 10.05 10.5 0.2 10.8 10.2 S4 Sg 0.9 0.1 So ay r=100 r: 100 ruo 0.8 0.9 0.1 i. ii. Use value iteration algorithm and compute state values. Based on the state values determine the optimal policies from each state. Q.1. Consider the following MDP model of a state-space system. DISCOUNT FACTOR Y= 0.99 0.5 0.5 Si r:-5 S2 S3 03 r: -100 dy r: 10 0.95 0.5 10.05 10.5 0.2 10.8 10.2 S4 Sg 0.9 0.1 So ay r=100 r: 100 ruo 0.8 0.9 0.1 i. ii. Use value iteration algorithm and compute state values. Based on the state values determine the optimal policies from each state