elect the correct choice below and fill in the answer boxes to your choice.

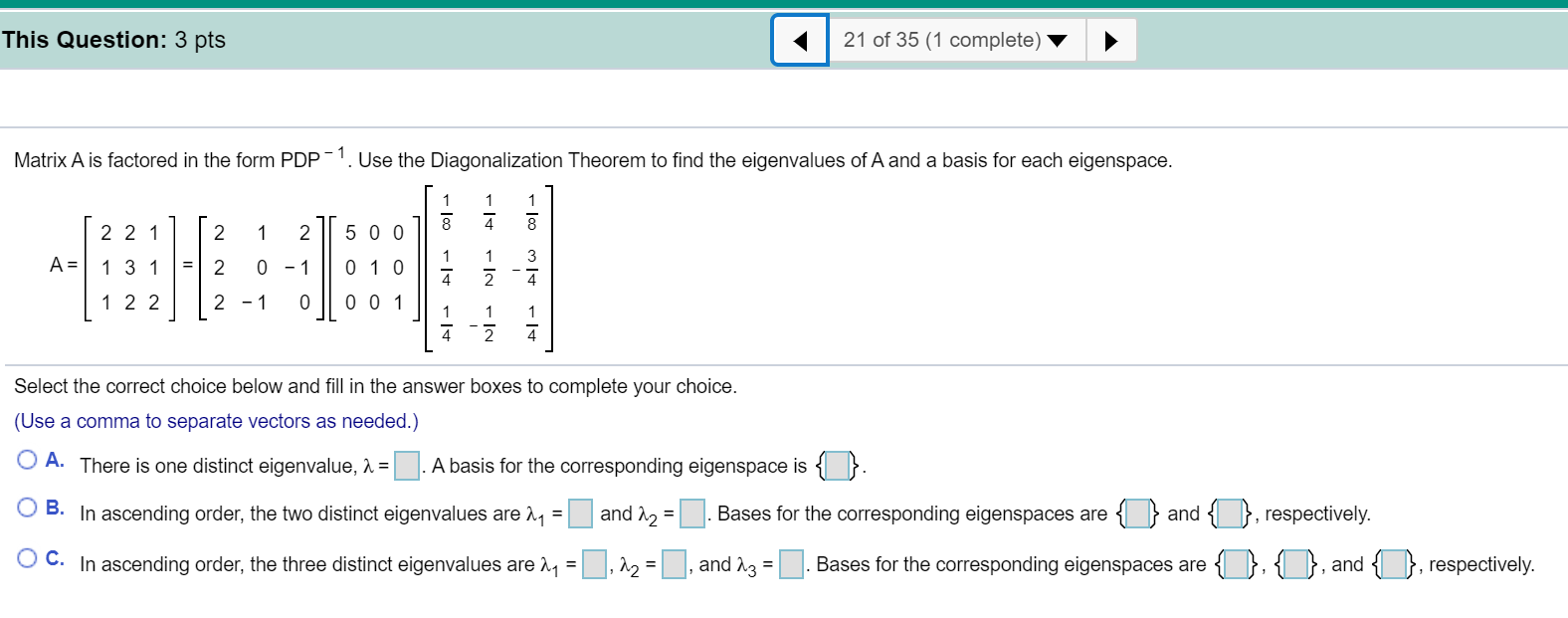
This Question: 3 pts 21 of 35 (1 complete) Matrix A is factored in the form PDP - 1. Use the Diagonalization Theorem to find the eigenvalues of A and a basis for each eigenspace. 2 2 1 2 50 0 col - Al - col - A = 13 0 - 1 0 10 1 - 4 2 2 2 0 0 1 AlW Al - Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) O A. There is one distinct eigenvalue, 2 = . A basis for the corresponding eigenspace is O B. In ascending order, the two distinct eigenvalues are My = and 12 = . Bases for the corresponding eigenspaces are { } and { }, respectively. O C. In ascending order, the three distinct eigenvalues are My = , 2 = , and 23 = . Bases for the corresponding eigenspaces are {} {}, and , respectively