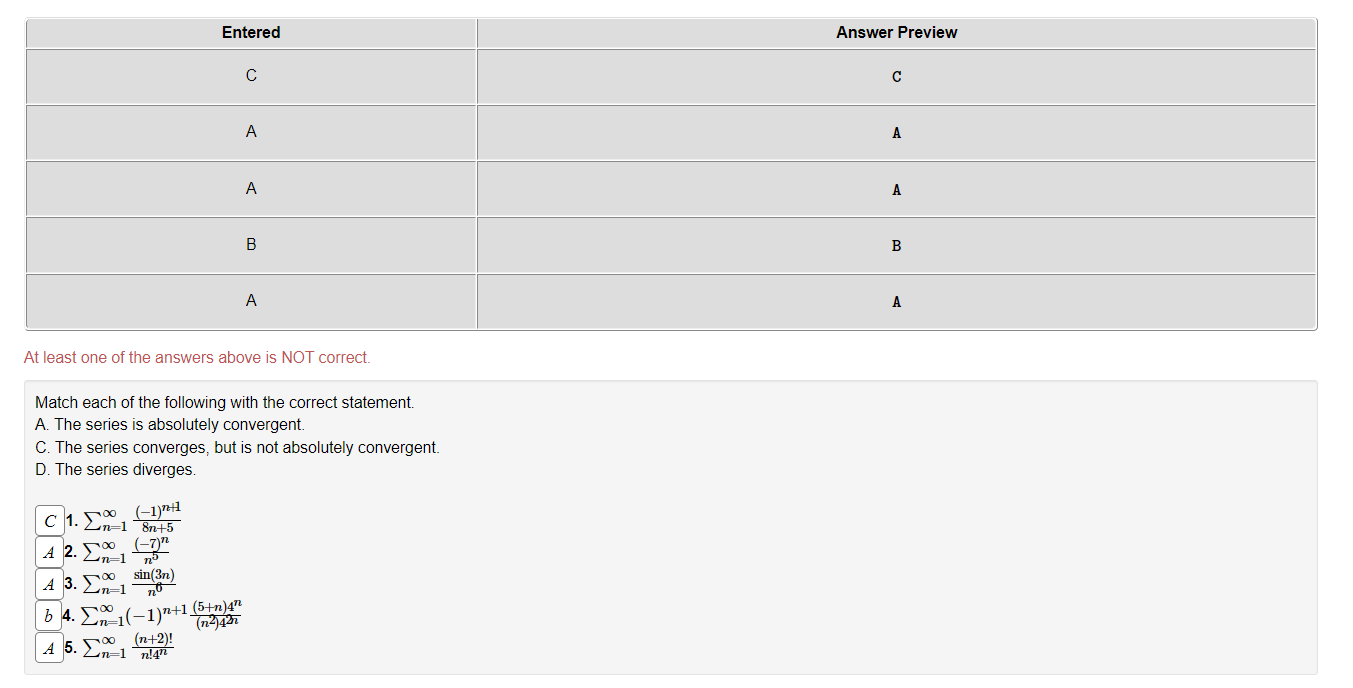
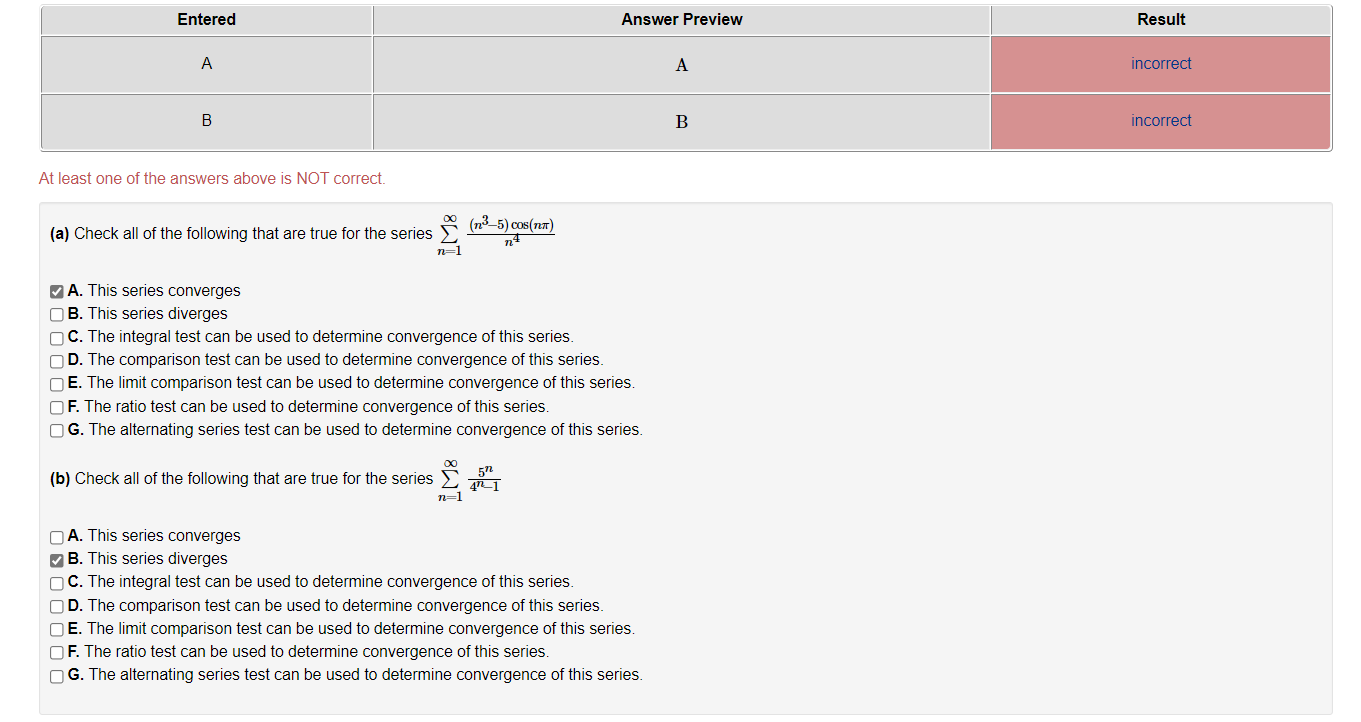
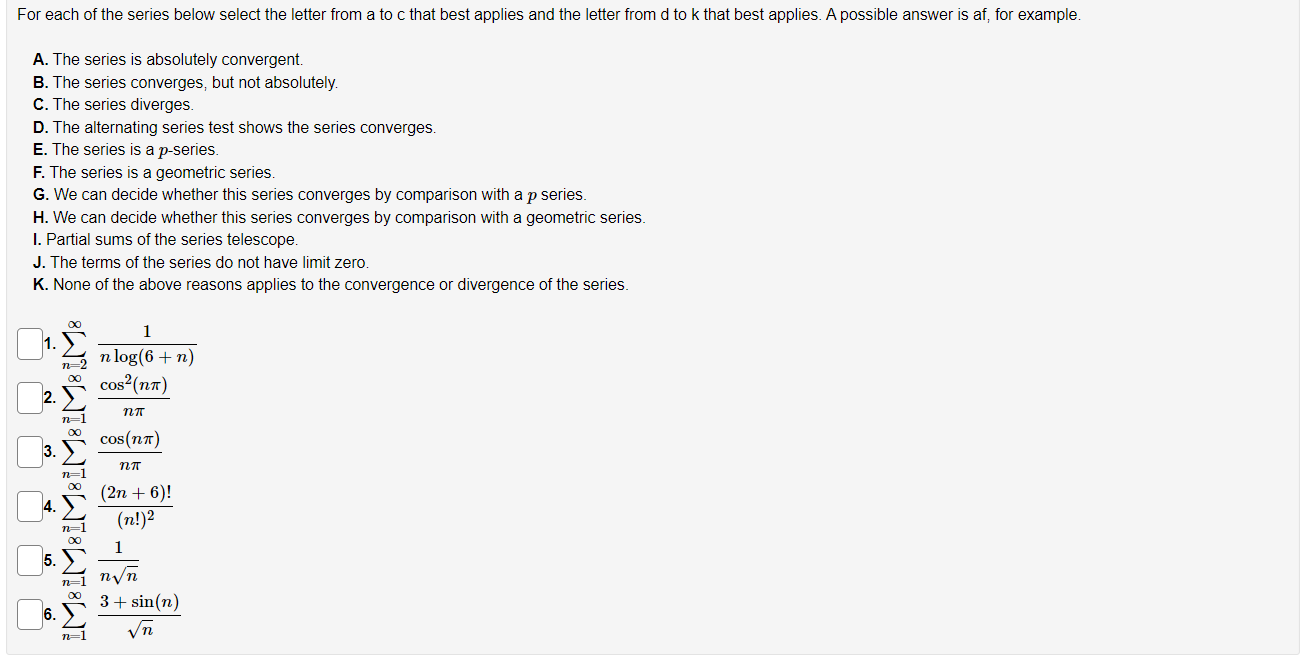
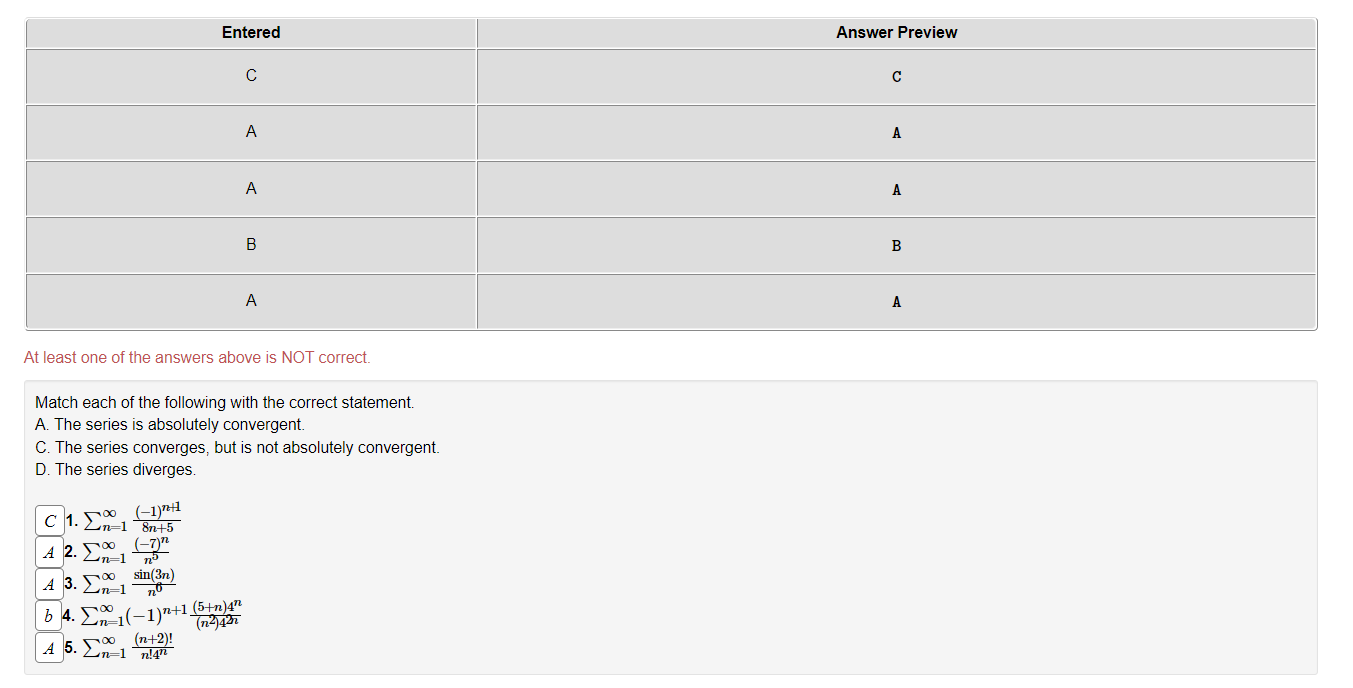
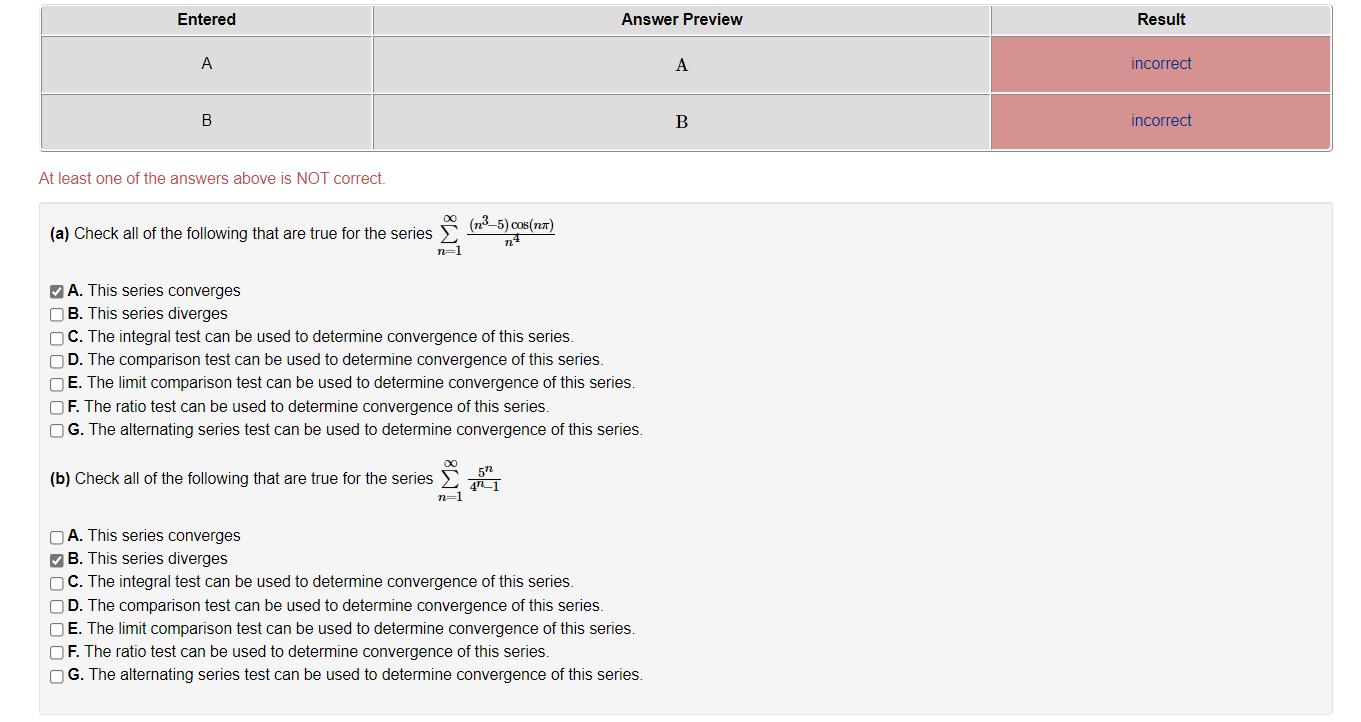
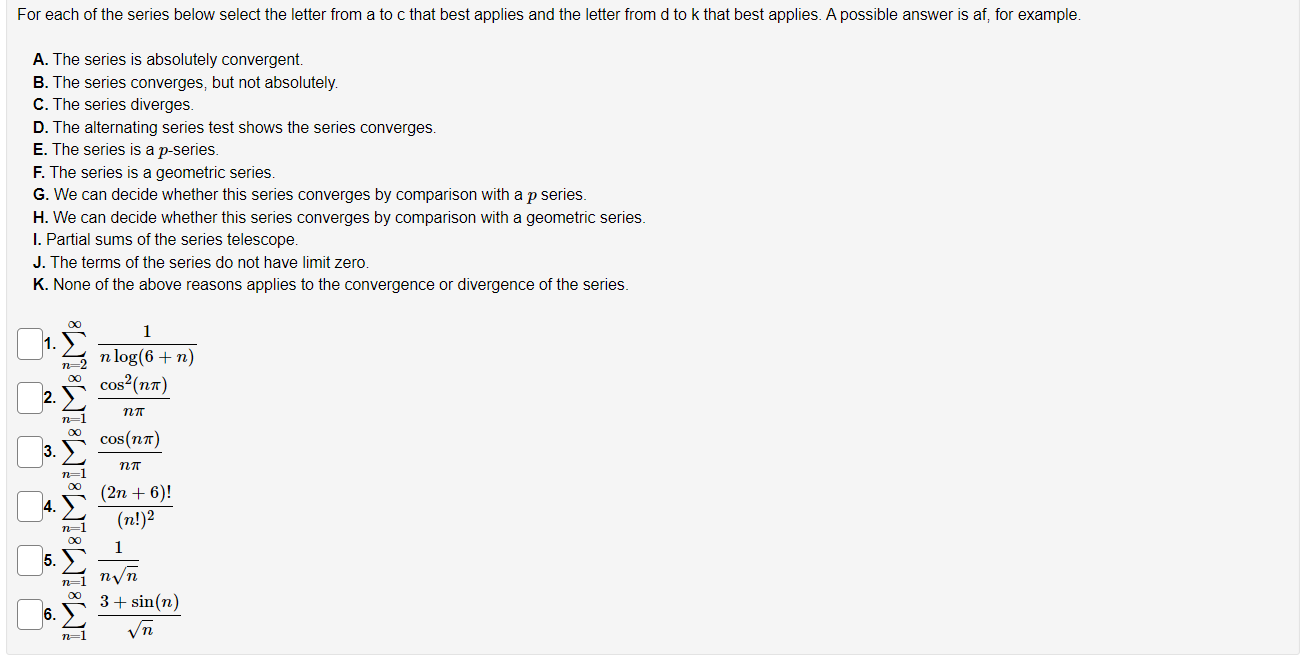
Entered Answer Preview C C A A A B B A A At least one of the answers above is NOT correct. Match each of the following with the correct statement. A. The series is absolutely convergent. C. The series converges, but is not absolutely convergent. D. The series diverges. C 1. So (-1)24 Un=1 8n+5 A 2. 0O (-7)n Un=1 4 3. No sin(37) . Zn=1 b 4. So n 1(-1)n+1 (5+n)in (n4437 4 5. 5 0o (n+2)! un=1 n!472Entered Answer Preview Result A A incorrect B B incorrect At least one of the answers above is NOT correct. (a) Check all of the following that are true for the series 90 (723-5) coS (TEXT ) n4 A. This series converges O B. This series diverges C. The integral test can be used to determine convergence of this series. OD. The comparison test can be used to determine convergence of this series. E. The limit comparison test can be used to determine convergence of this series. OF. The ratio test can be used to determine convergence of this series O G. The alternating series test can be used to determine convergence of this series. (b) Check all of the following that are true for the series _ n= 1 A. This series converges B. This series diverges OC. The integral test can be used to determine convergence of this series. O D. The comparison test can be used to determine convergence of this series. OE. The limit comparison test can be used to determine convergence of this series. OF. The ratio test can be used to determine convergence of this series. OG. The alternating series test can be used to determine convergence of this series.For each of the series belowr select the letter from a to c that best applies and the letter from d to k that best applies. A possible answer is af, for example. A. The series is absolutely convergent. B. The series converges, but not absolutely. C. The series diverges. D. The alternating series test shows the series converges. E. The series is a pseries. F. The series is a geometric series. G. We can decide whether this series converges by comparison with a 33 series. H. We can decide whether this series converges by comparison with a geometric series. I. Partial sums of the series telescope. J. The terms of the series do not have limit zero. K. None of the above reasons applies to the convergence or divergence of the series. \"0 1 _1- E2 nlog(6 +11) 72- i0: 0032(n7r) 7 11:1 7371' 00 003(1111') _3.Z; 7\" i m {2n+6)! _4.; (n!}2 _ m 1 5. g m B Z 3+sm(n] -n=1