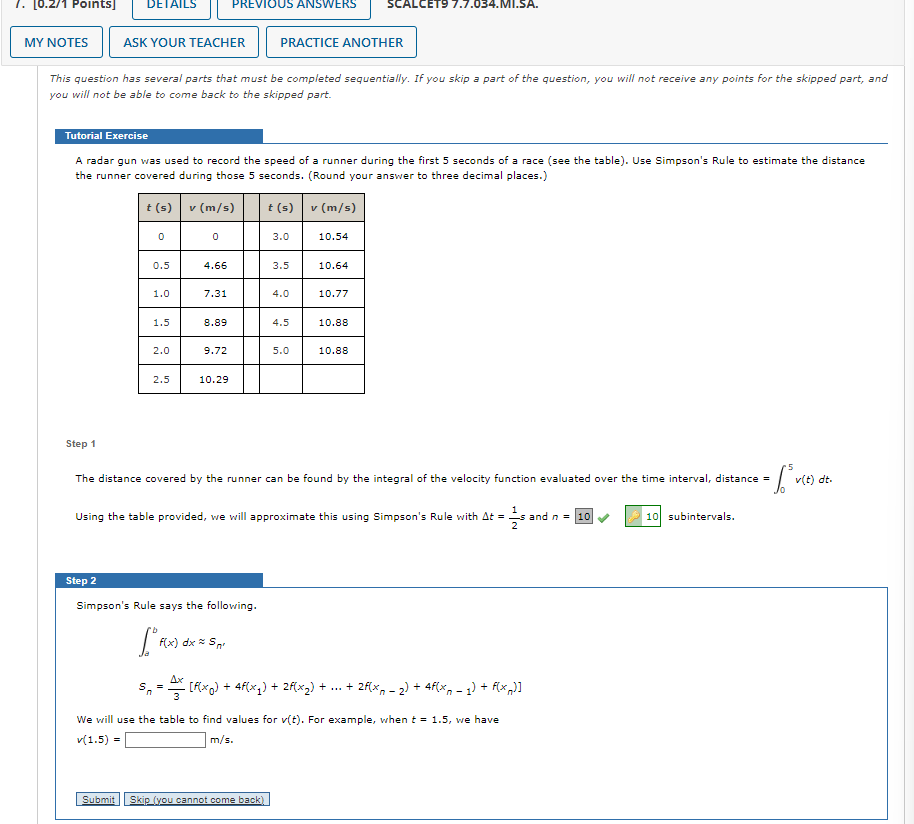
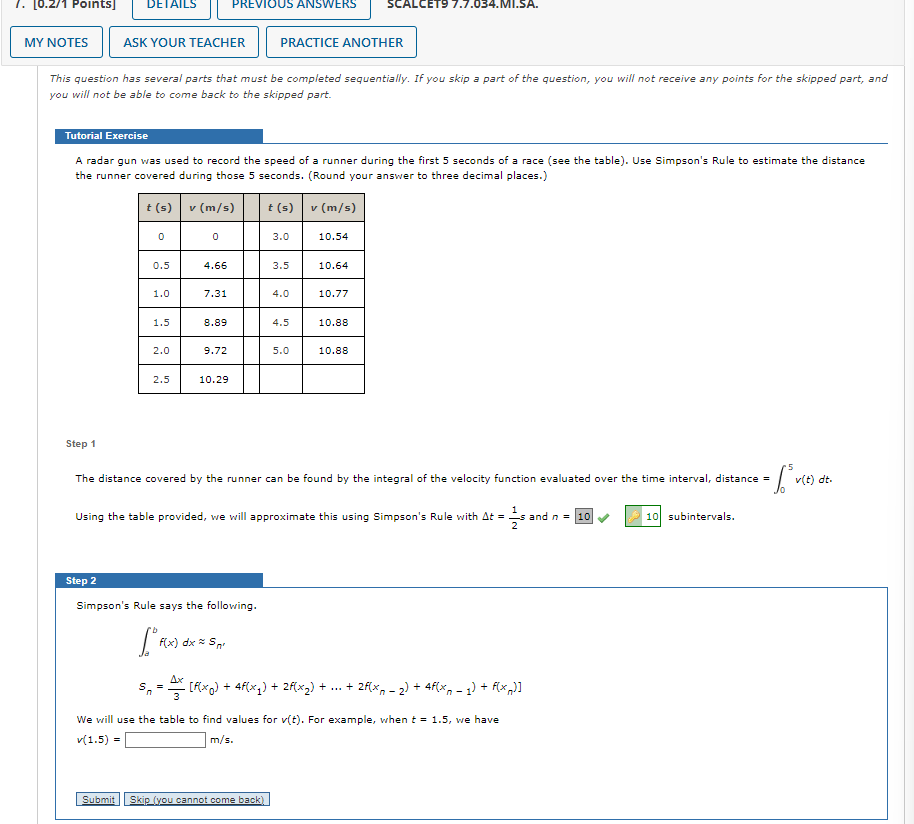
ERS MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part. Tutorial Exercise A radar gun was used to record the speed of a runner during the first 5 seconds of a race (see the table). Use Simpson's Rule to estimate the distance the runner covered during those 5 seconds. (Round your answer to three decimal places.) t (5) v (m/s) t (5) v (m/s) 0 3.0 10.54 0.5 4.66 3. 10.6 1. 7.31 4. 10.7 1.5 8.89 4.5 10.88 2.0 9.72 5.0 10.8 2.5 10.29 Step 1 The distance covered by the runner can be found by the integral of the velocity function evaluated over the time interval, distance = ( "v(t) dt. Using the table provided, we will approximate this using Simpson's Rule with At = = and n = 10| # 10 subintervals. Step 2 Simpson's Rule says the following. 5, = _ [R(xq) + 4f(x]) + 2f(x2) + ... + 2f(*, - 2) + 4f(*, - 1) + f(x,)] We will use the table to find values for v(t). For example, when : = 1.5, we have V(1.5) = m/s. Submit |Skip (you cannot come back)