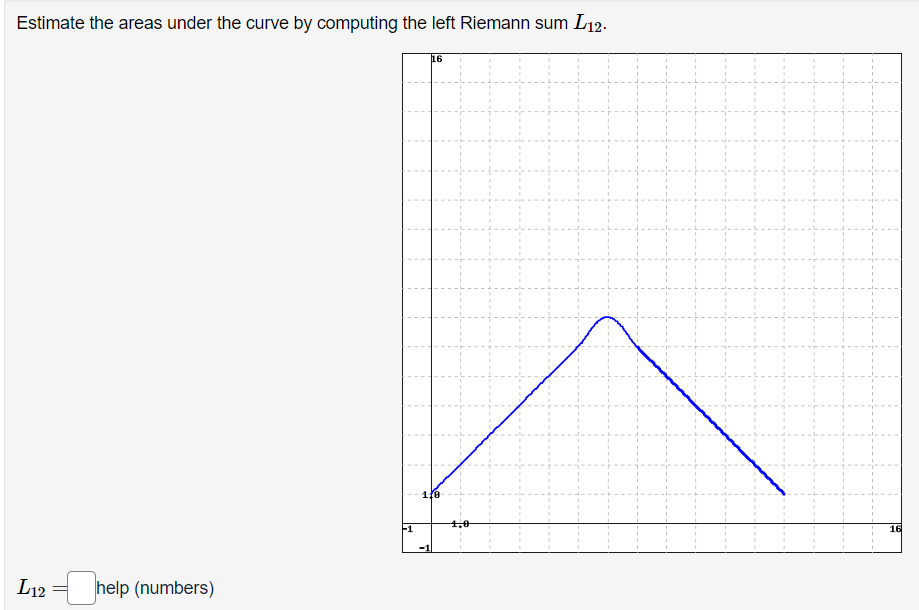
Question: Estimate the areas under the curve by computing the left Riemann sum L12. 16 L12 help (numbers)Estimate the areas under the curve by computing the
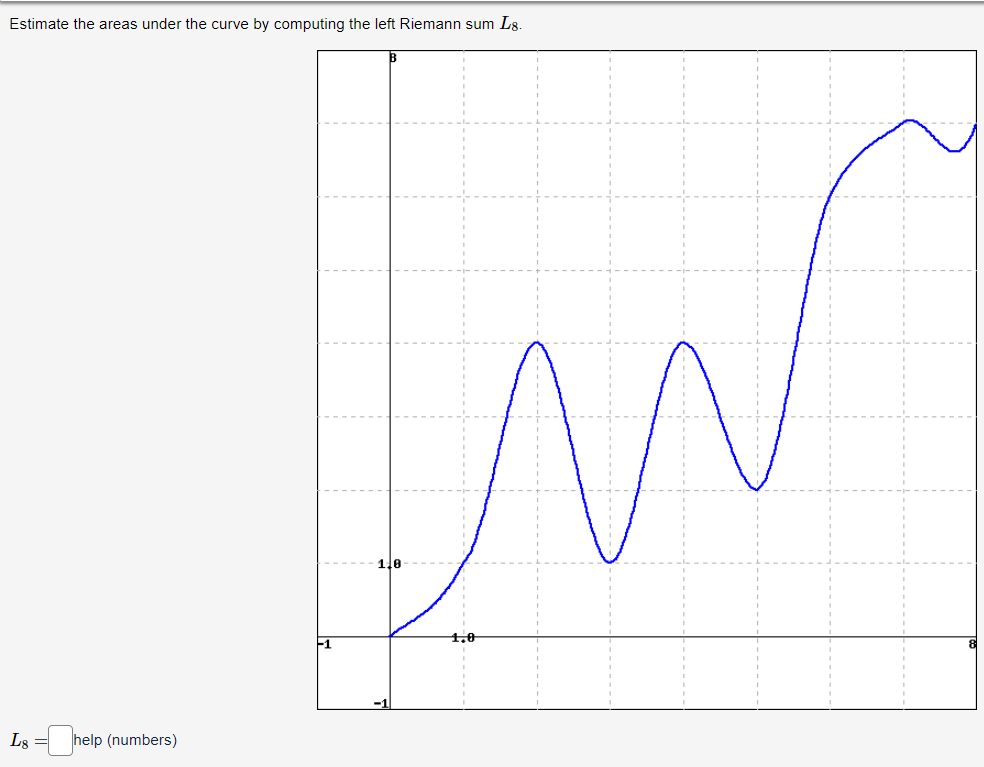
![computing the left Riemann sum Lg. Lg :':_]help (numbers) Given the function,](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/670a2d70b6230_240670a2d70a3083.jpg)


![[1,5] if the heights of the rectangles are found by evaluating the](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/670a2d71b71aa_241670a2d71a62a4.jpg)

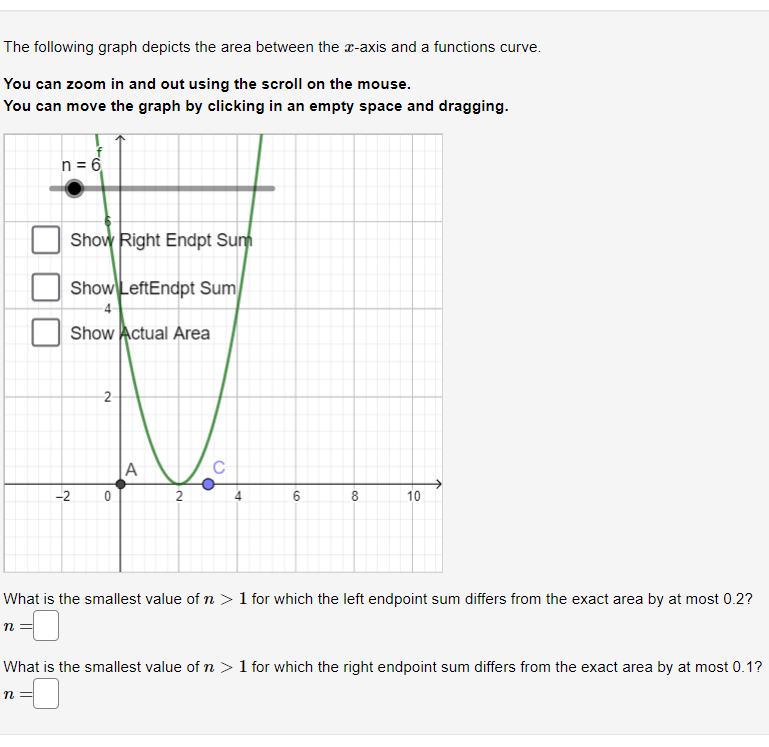

Estimate the areas under the curve by computing the left Riemann sum L12. 16 L12 help (numbers)Estimate the areas under the curve by computing the left Riemann sum Lg. Lg :':_]help (numbers) Given the function, f(z) = .7:2, using 6 rectangles of equal width, find an approximation to the area between the curve and the z-axis over the interval [1,5] if the heights of the rectangles are found by evaluating the function at the left endpoints, right endpoints, and midpoints of each subinterval created by a partition of the interval given. Using left endpoints, the approximate area is: | | Using right endpoints, the approximate area is: | | Using midpeints, the approximate area is | ' Given the function, f(z) = z 4 5w2, using 6 rectangles of equal width, find an approximation to the area between the curve and the x-axis over the interval [1, 5] if the heights of the rectangles are found by evaluating the function at the left endpoints, right endpoints, and midpoints of each subinterval created by a partition of the interval given. Using left endpoints, the approximate area is: | 50.8148 ' Using right endpoints, the approximate area is: | 43148 ' Using midpoints, the approximate area is: ' 31.2592 | Given the function, f(z) = % using 6 rectangles of equal width, find an approximation to the area between the curve and the x-axis over the interval [4, 10] if the heights of the rectangles are found by evaluating the function at the left endpoints, right endpoints, and midpoints of each subinterval created by a partition of the interval given. Using left endpoints, the approximate area is: | | Using right endpoints, the approximate area is: | | Using midpoints, the approximate area is: | | Suppose f(x) = 8 a. The rectangles in the graph on the left illustrate a left endpoint Riemann sum for f() on the interval 3 1 for which the left endpoint sum differs from the exact area by at most 0.27 n=_ | What is the smallest value of n > 1 for which the right endpoint sum differs from the exact area by at most 0.1? n= | Evaluate / (12 - 0)(42 - 3) d (+2 -9)(t2 - 3) dt using the Fundamental Theorem of Calculus, Part 2. Enter only exact answers. (12 -9)(12 - 3) dt = help (numbers)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


