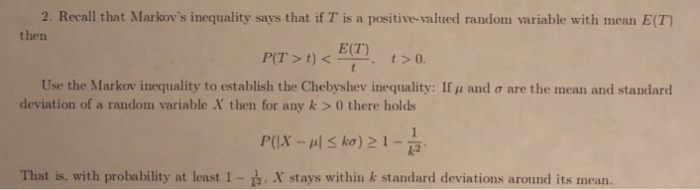
estion:

Calculate the weighted average cost of capital (WACC) for PDI.

E/V80.00%

Cost of equity9.40%

Risk-free rate 3.00%

Beta 1.28

Market equity risk premium 5.00%

D/V20.00%

Cost of debt4.00%

Corporate tax rate40.00%

WACC 80% x 9.40%) + [20% x 4% x (1 - 40%)]= 8.00% WACC = (E/V x Re) + ((D/V x Rd) x (1 - T))

*Cost of equityRisk free rate of return + (Beta * Risk premium) = 3% + (1.28 x 5%) 0.094

Givend the above, I cannot get the following:

Sum of FCF PV =?

Terminal value =?

Present value of terminal value =?

Total value of PDI =?

Assumptions

Discount rate ?

Terminal value ?

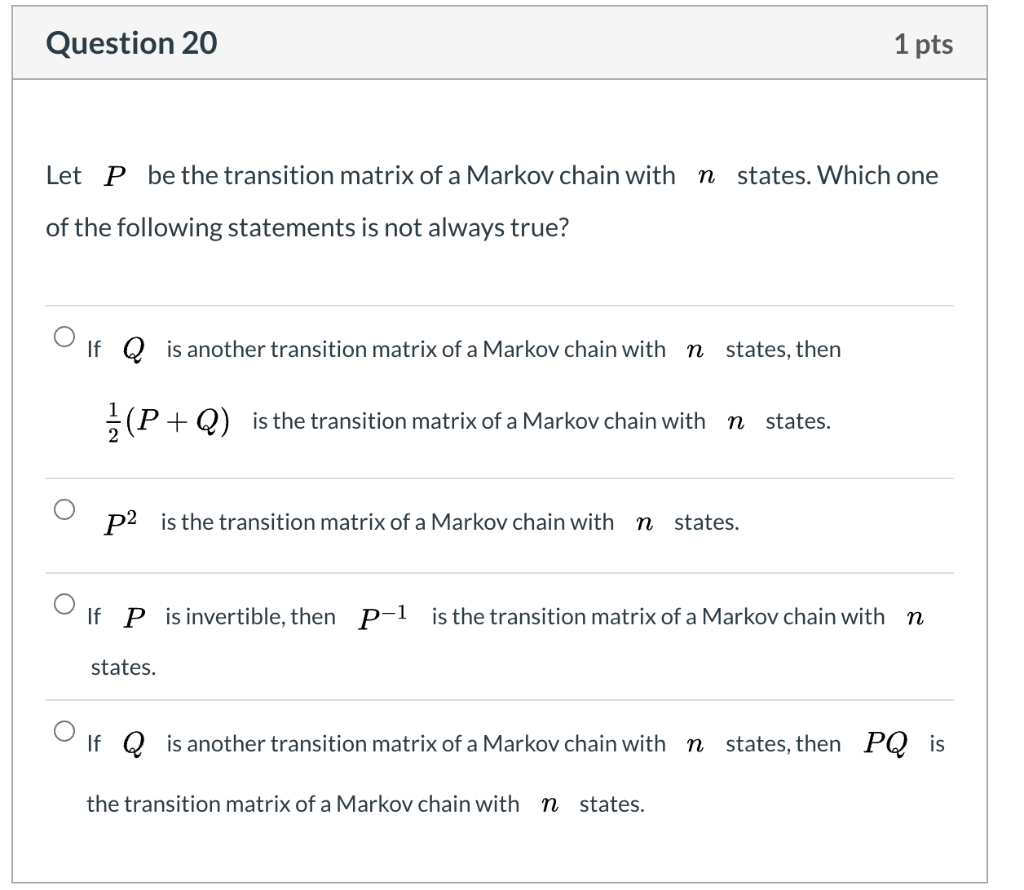
Let P be the transition matrix of a Markov chain with 7 states. Which one of the following statements is not always true? O p2 is the transition matrix of a Markov chain with 72 states. If O is another transition matrix of a Markov chain with 72 states, then PQ is the transition matrix of a Markov chain with 72 states. O If ) is another transition matrix of a Markov chain with 72 states, then *(P + Q) is the transition matrix of a Markov chain with 7, states. If P is invertible, then p-1 is the transition matrix of a Markov chain with 71, states.Question 20 1 pts Let P be the transition matrix of a Markov chain with n states. Which one of the following statements is not always true? If Q is another transition matrix of a Markov chain with n states, then =(P + Q) is the transition matrix of a Markov chain with n states. O P2 is the transition matrix of a Markov chain with n states. If P is invertible, then p-1 is the transition matrix of a Markov chain with n states. If Q is another transition matrix of a Markov chain with n states, then PQ is the transition matrix of a Markov chain with n states.2. Recall that Markov's inequality says that if T' is a positive-valued random variable with mean E(T) then E(T) P(T > 1 ) 0 there holds P(1X - #| Ska) 21 - 1 That is. with probability at least 1 - 2. X stays within & standard deviations around its mean