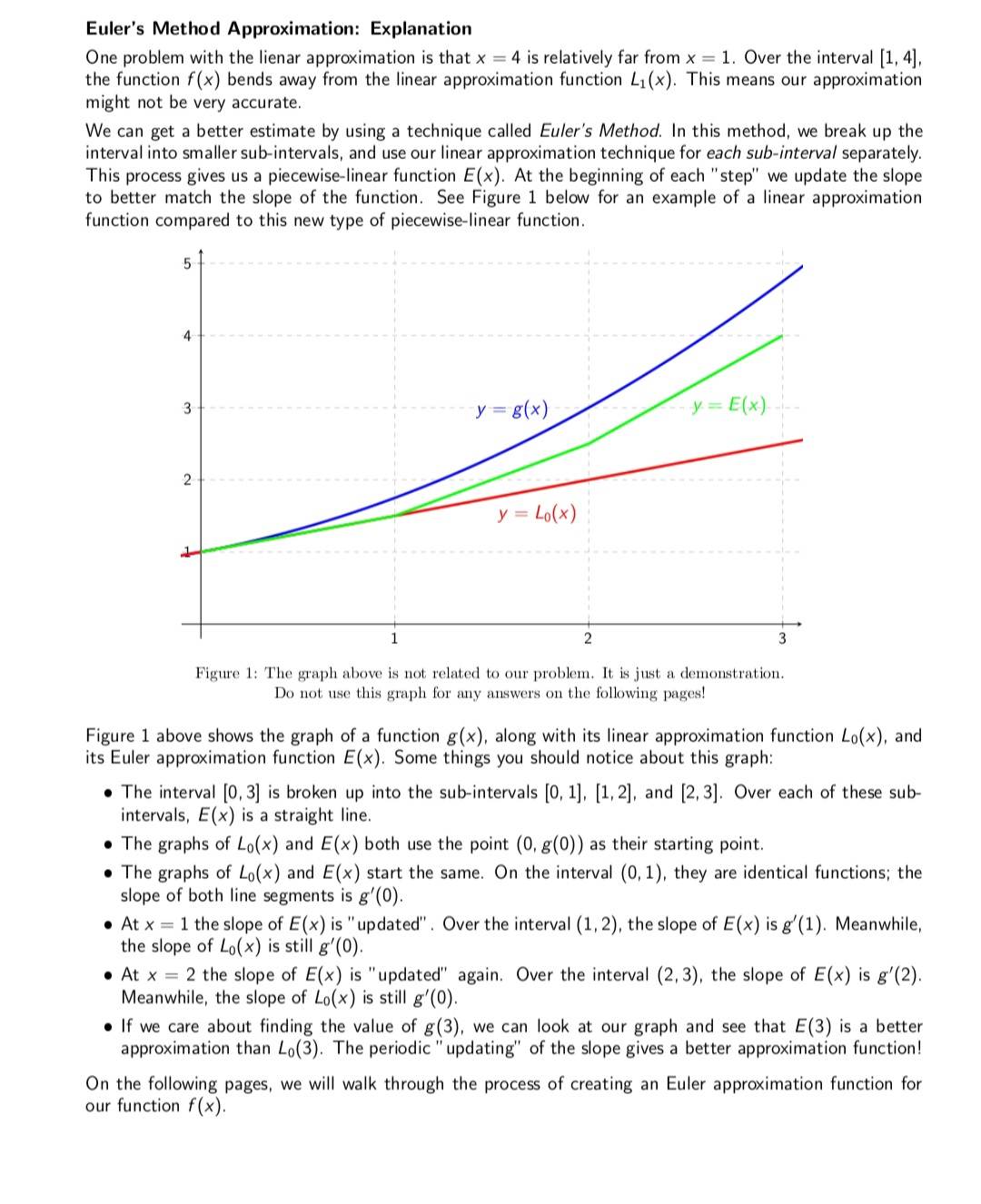
Euler's Method Approximation: Explanation One problem with the lienar approximation is that x = 4 is relatively far from x = 1. Over the interval [1, 4], the function f(x) bends away from the linear approximation function L(x). This means our approximation might not be very accurate. We can get a better estimate by using a technique called Euler's Method. In this method, we break up the interval into smaller sub-intervals, and use our linear approximation technique for each sub-interval separately. This process gives us a piecewise-linear function E(x). At the beginning of each "step" we update the slope to better match the slope of the function. See Figure 1 below for an example of a linear approximation function compared to this new type of piecewise-linear function. 5 4 3 y = g(x) y= E(x) 2 y = Lo(x) 1 3 Figure 1: The graph above is not related to our problem. It is just a demonstration. Do not use this graph for any answers on the following pages! Figure 1 above shows the graph of a function g(x), along with its linear approximation function Lo(x), and its Euler approximation function E(x). Some things you should notice about this graph: The interval [0,3] is broken up into the sub-intervals [0, 1], [1, 2], and [2, 3]. Over each of these sub- intervals, E(x) is a straight line. The graphs of Lo(x) and E(x) both use the point (0, g(0)) as their starting point. The graphs of Lo(x) and E(x) start the same. On the interval (0, 1), they are identical functions; the slope of both line segments is g'(0). At x 1 the slope of E(x) is "updated". Over the interval (1, 2), the slope of E(x) is g'(1). Meanwhile, the slope of Lo(x) is still g'(0). At x 2 the slope of E(x) is "updated" again. Over the interval (2, 3), the slope of E(x) is g'(2). Meanwhile, the slope of Lo(x) is still g'(0). If we care about finding the value of g(3), we can look at our graph and see that E(3) is a better approximation than Lo(3). The periodic "updating" of the slope gives a better approximation function! On the following pages, we will walk through the process of creating an Euler approximation function for our function f(x). c) (5 points) We have now found values for bo, mo, and m. Use these to find a value for b which makes E(x) continuous at x = 2. Make sure you use the definition of continuity. b = = d) (5 points) We have now found values for b, m, and m2. Use these to find a value for b which makes E(x) continuous at x = 3. Make sure you use the definition of continuity. b = e) (3 points) We've now found all of the necessary constants. Summarize your findings by filling in the following for E(x): E(x) = f) (3 points) Use the function E(x) to approximate f(4). f(4) if 1x2 if 2