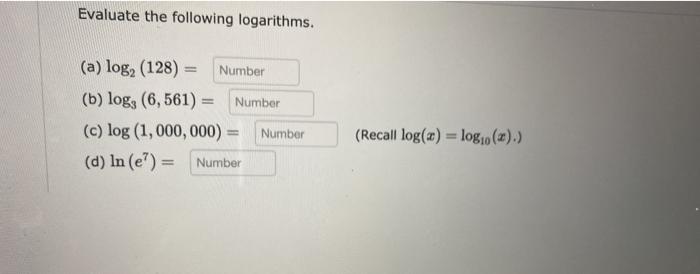
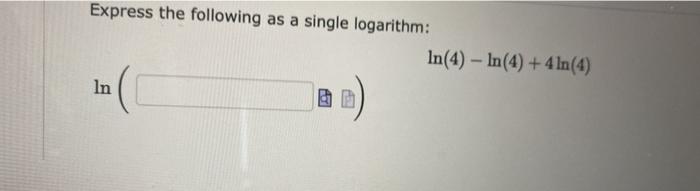
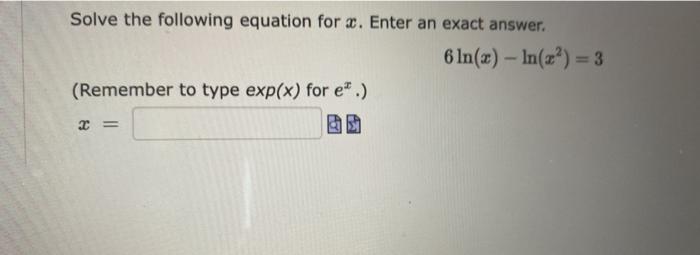
Evaluate the following logarithms. (a) log (128) Number (b) log, (6,561) (c) log (1, 000, 000) = (d) In (e7) = Number Number Number (Recall log(a) = log0 (2).) Express the following as a single logarithm: In BD In(4) In (4) + 4 ln(4) Solve the following equation for x. Enter an exact answer. (Remember to type exp(x) for e.) x= 6 ln(x) - In(2) = 3 A radioactive element has a half-life of 8 days. This means that the amount of the radioactive element in a given sample halves every 8 days. (a) Suppose a sample initially contains 300 mg of the radioactive element. How much remains after 56 days? (Answer to one decimal place.) Number mg (b) How many days will it take for the sample to be reduced to 60 mg? (Answer to one decimal place.) Number days