Question: Evaluate the function f(x) at the given numbers (correct to six decimal places). f(x)=(x^(2)-3x)/(x^(2)-x-6),x=3.5,3.1,3.05,3.01,3.005,3.001,2.9,2.95,2.99,2.995,2.999 f(3.5)= f(3.1)= f(3.05)= f(3.01)= f(3.005)=
Evaluate the function
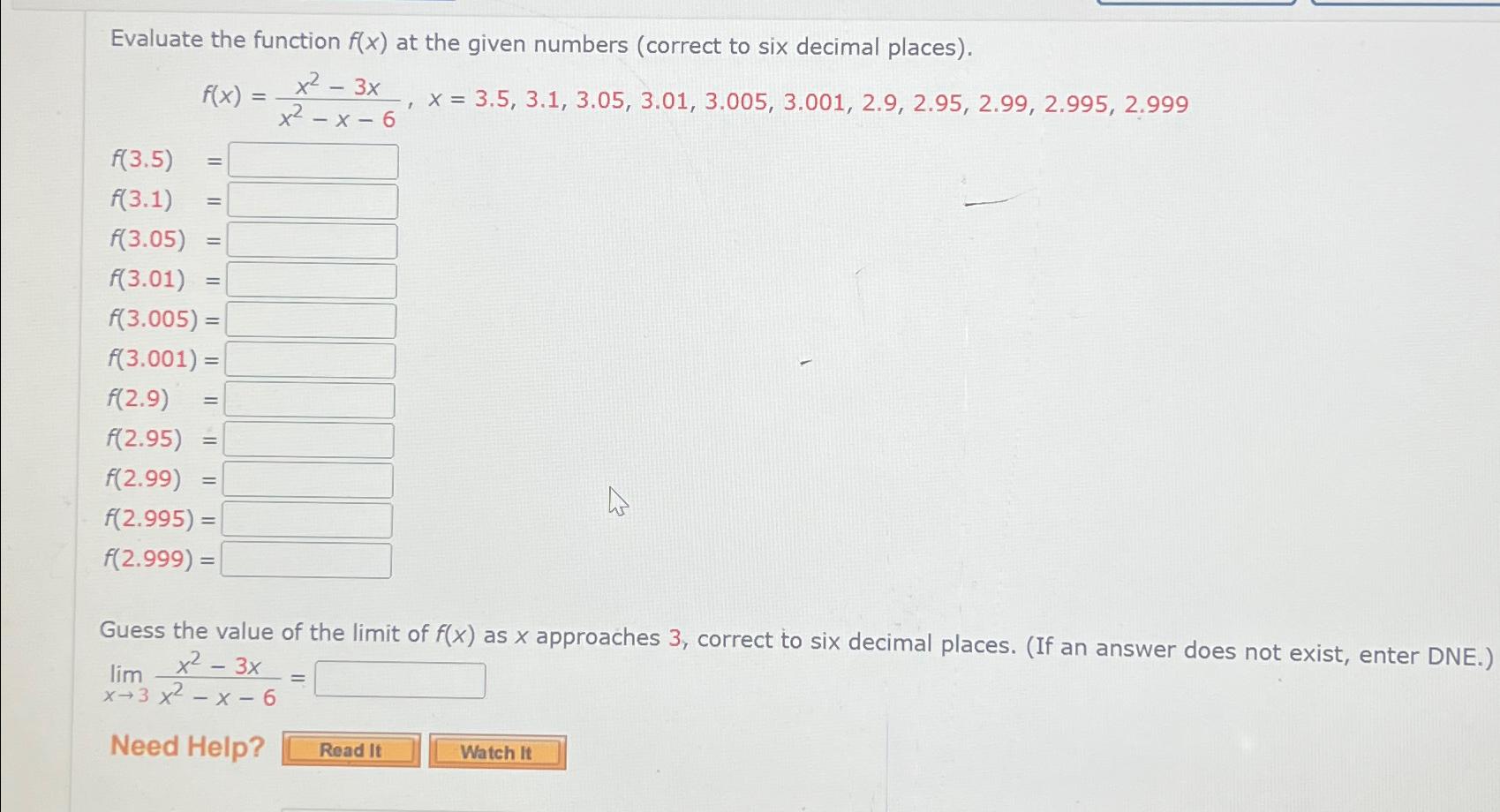
f(x)at the given numbers (correct to six decimal places).\
f(x)=(x^(2)-3x)/(x^(2)-x-6),x=3.5,3.1,3.05,3.01,3.005,3.001,2.9,2.95,2.99,2.995,2.999\
f(3.5)=\
f(3.1)=\
f(3.05)=\
f(3.01)=\
f(3.005)=\
f(3.001)=\
f(2.9)=\
f(2.95)=\
f(2.99)=\
f(2.995)=\
f(2.999)=\ Guess the value of the limit of
f(x)as
xapproaches 3 , correct to six decimal places. (If an answer does not exist, enter DNE.)\
\\\\lim_(x->3)(x^(2)-3x)/(x^(2)-x-6)=\ Need Help?
Evaluate the function f(x) at the given numbers (correct to six decimal places). f(x)=x2x6x23x,x=3.5,3.1,3.05,3.01,3.005,3.001,2.9,2.95,2.99,2.995,2.999 f(3.5)=f(3.1)=f(3.05)=f(3.01)=f(3.005)=f(3.001)=f(2.9)=f(2.95)=f(2.99)=f(2.995)=f(2.999)= Guess the value of the limit of f(x) as x approaches 3 , correct to six decimal places. (If an answer does not exist, enter DNE.) limx3x2x6x23x=
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock
Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock
Study Help