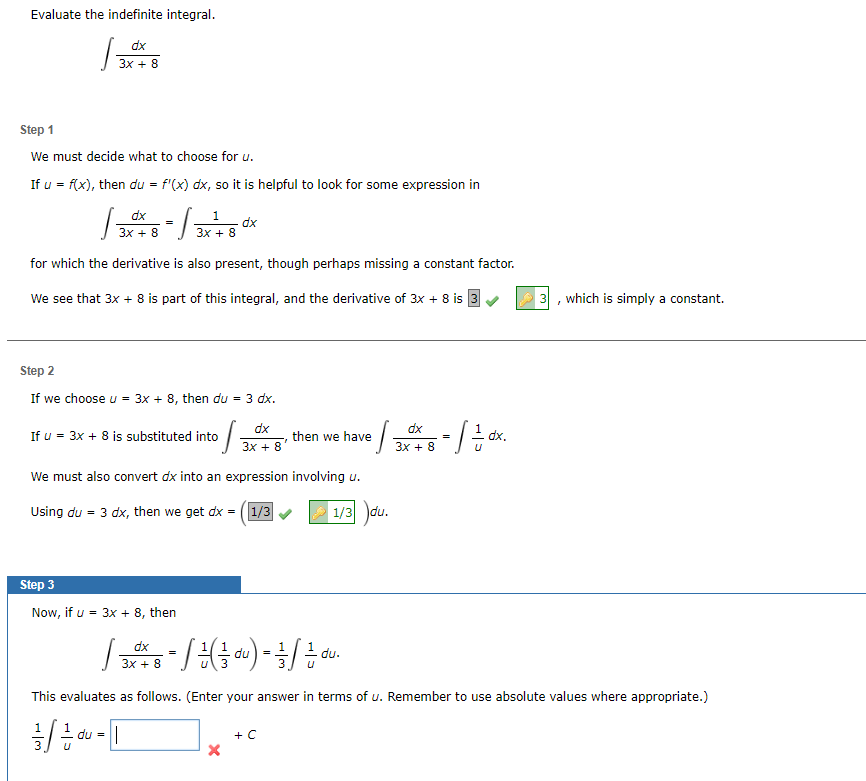
Evaluate the indefinite integral. dx 3x + 8 Step 1 We must decide what to choose for u. If u = f(x), then du = f'(x) dx, so it is helpful to look for some expression in dx 3x + 8 = - /= 1 dx 3x + 8 for which the derivative is also present, though perhaps missing a constant factor. We see that 3x + 8 is part of this integral, and the derivative of 3x + 8 is 3 Step 2 If we choose u = 3x + 8, then du = 3 dx. dx then we have 3x + 8 / dx = 3x + 8 If u = 3x + 8 is substituted into 33 We must also convert dx into an expression involving u. Using du = 3 dx, then we get dx = (1/3 1/3 )du. 3 ' which is simply a constant. Step 3 Now, if u = 3x + 8, then dx 3x + 8 == (du) = 1 du. This evaluates as follows. (Enter your answer in terms of u. Remember to use absolute values where appropriate.) du = || + C