evaluate the integral and explain clearly how you are applying Theorem 3.3.4.Theorem 3.3.4:(Independence of Path) Let

f

be a continuous complex-valued\ function on a region

\\\\Omega

. Then the following assertions are equivalent:\ (a) There is an analytic function

F

on

\\\\Omega

such that

f(z)=F^(')(z)

for all

z

in

\\\\Omega

.\ (b) For arbitrary points

z_(1),z_(2)

and any path

\\\\gamma

in

\\\\Omega

that joins

z_(1)

to

z_(2)

, the integral\

I=\\\\int_(\\\\gamma ) f(z)dz

\ is independent of the path

\\\\gamma

.\ (c) The integral of

f

over all closed paths is zero.\ Moreover, if (a) holds,

^(1)

then for any path

\\\\gamma

in

\\\\Omega

that joins

z_(1)

and

z_(2)

we have\

\\\\int_(\\\\gamma ) f(z)dz=F(z_(2))-F(z_(1))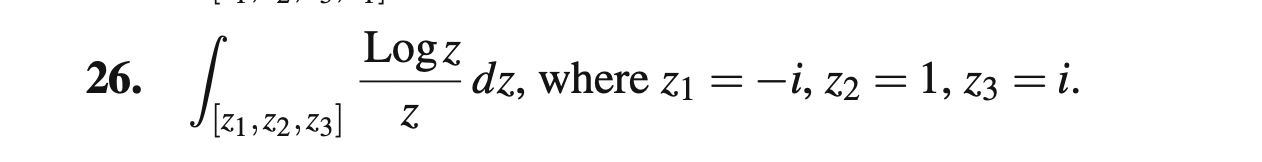

26. [z1,z2,z3]zlogzdz, where z1=i,z2=1,z3=i