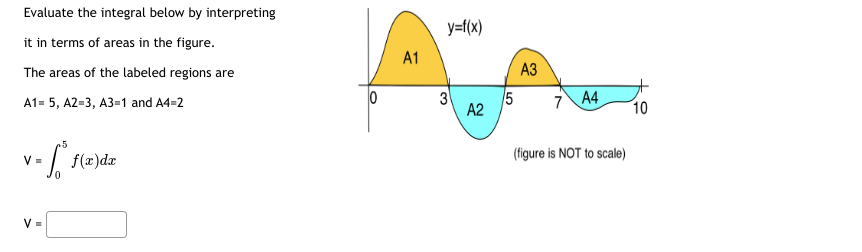
Question: Evaluate the integral below by interpreting y=f(x) it in terms of areas in the figure. A1 The areas of the labeled regions are A3 A1-



![object's velocity after tsecends is vEt] = 24 2t feet per second.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6666c988aa2a2_2966666c98898af0.jpg)

![to a stop {velocity I D]? [b] How far does the car](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6666c98929873_2976666c9891a2e3.jpg)


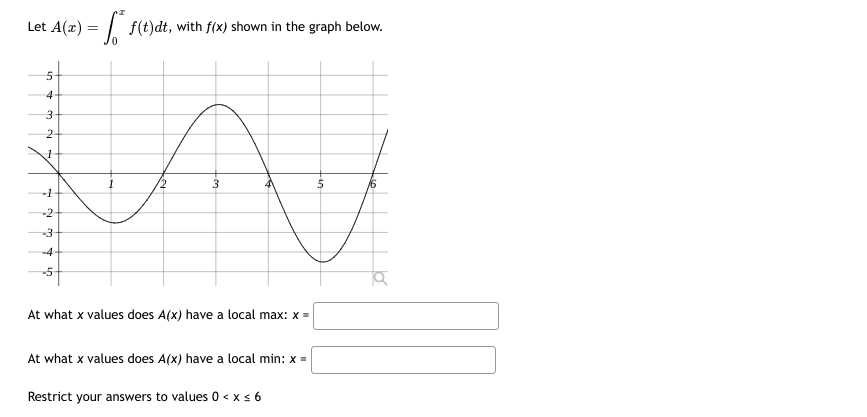
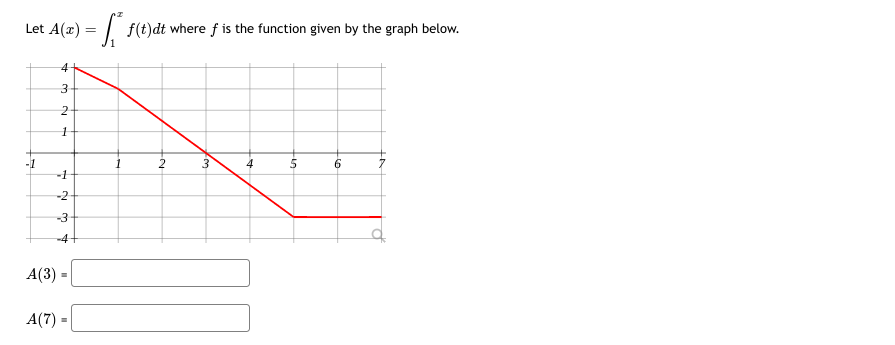
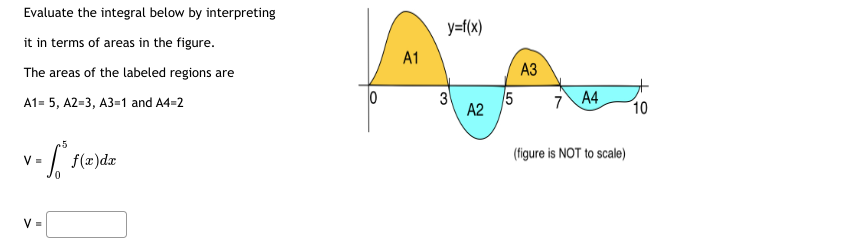








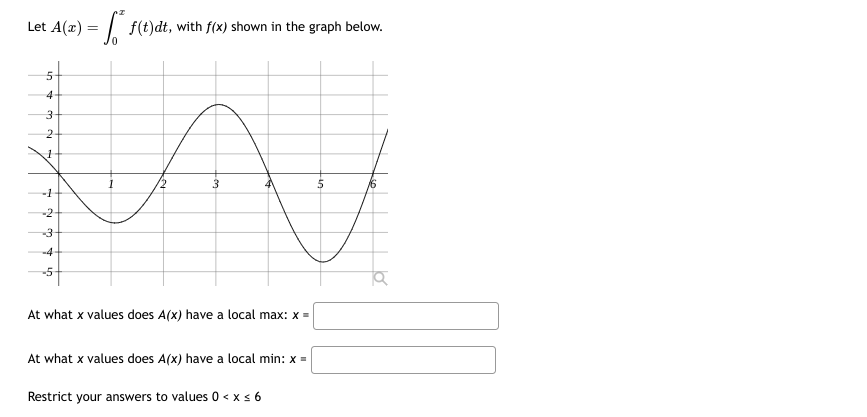
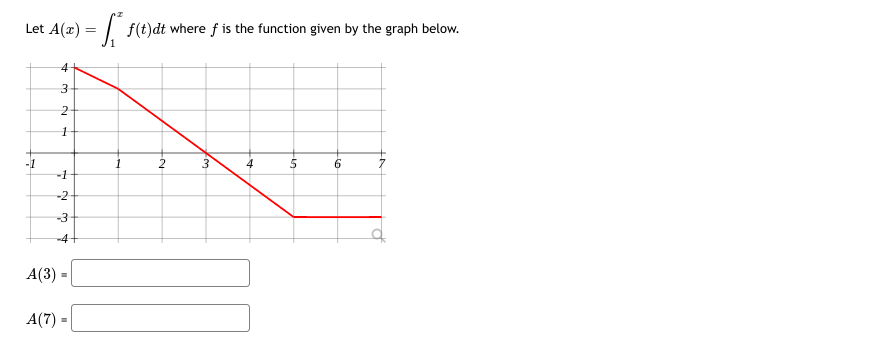
Evaluate the integral below by interpreting y=f(x) it in terms of areas in the figure. A1 The areas of the labeled regions are A3 A1- 5, A2-3, A3=1 and A4-2 O 5 A4 A2 7 10 .5 V = f(x)dx (figure is NOT to scale) V =\fAn object's velocity after tsecends is vEt] = 24 2t feet per second. {a} How many seconds does it take for the object to come to a stop {velocity I D]? [b] How far does the car travel during that time? {c} How many seconds does it take the car to travel half the distance in part (bi? Let A(x) = / f(t)dt, with f(x) shown in the graph below. At what x values does A(x) have a local max: x = At what x values does A(x) have a local min: x = Restrict your answers to values 0
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


