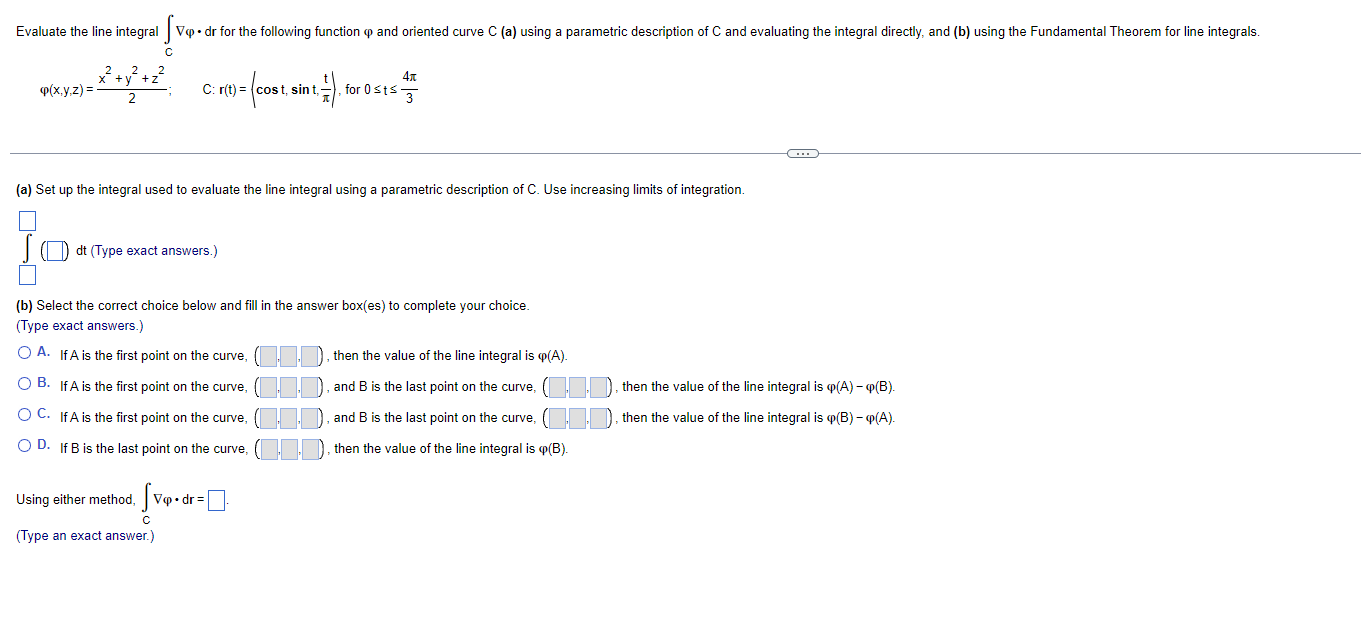
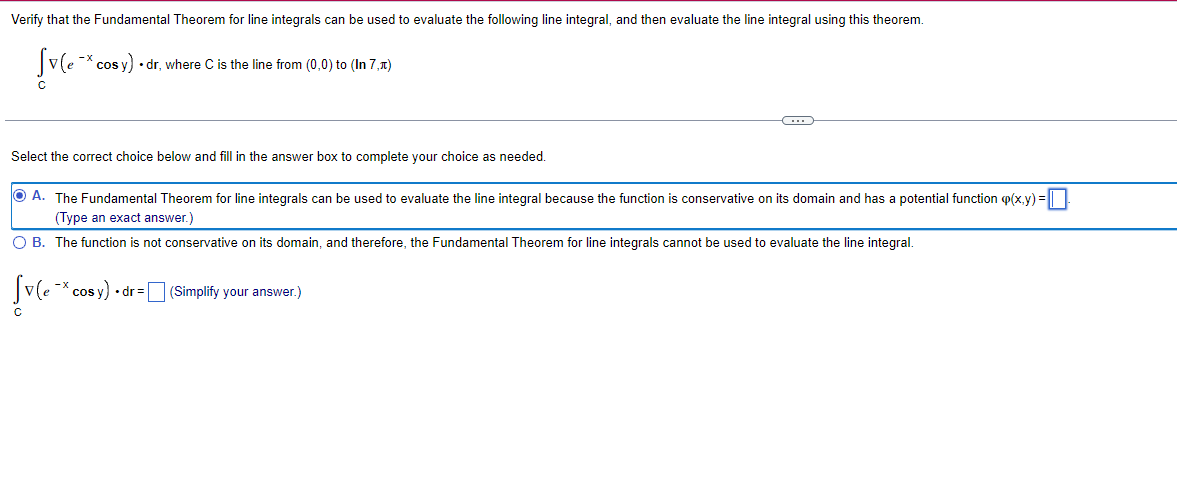
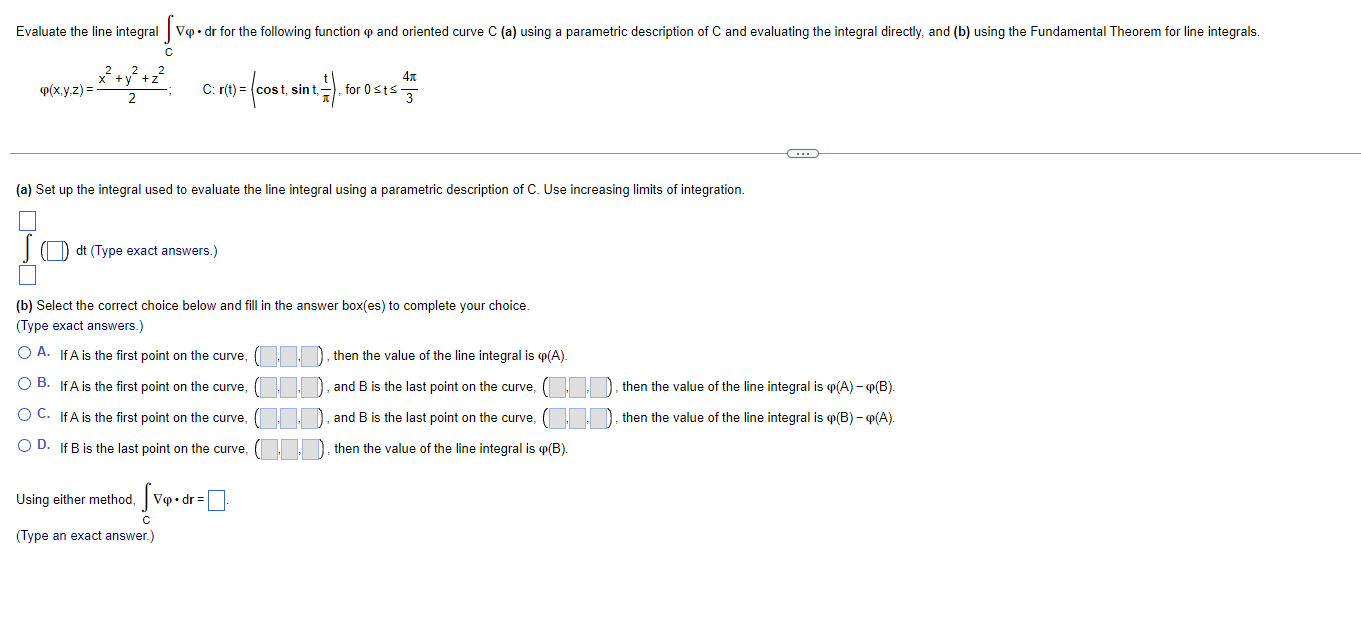
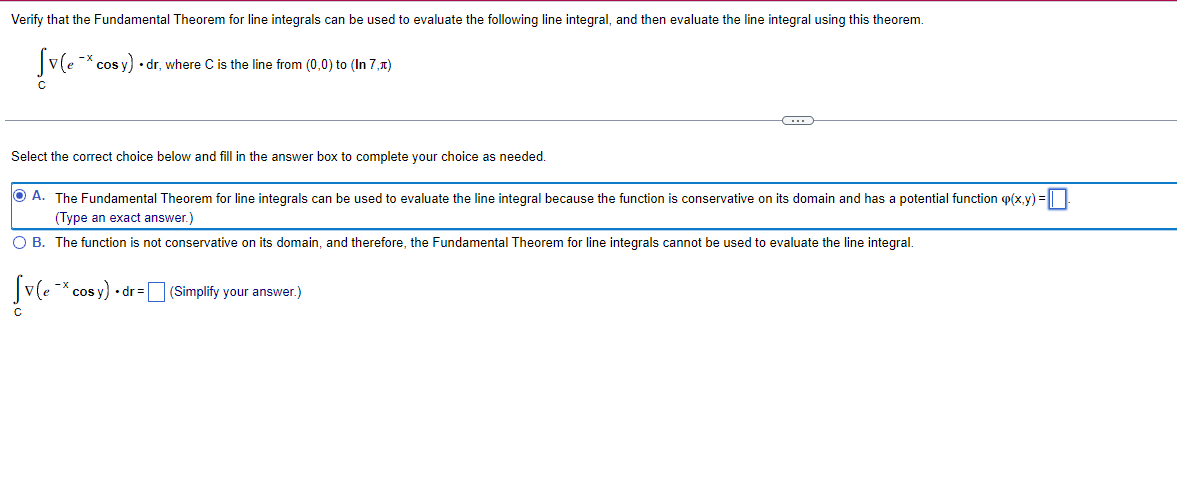
Evaluate the line integral |Vp . dr for the following function and oriented curve C (a) using a parametric description of C and evaluating the integral directly, and (b) using the Fundamental Theorem for line integrals. 2 +2 - 2 p(x,y,z) = 2 C: r(t ) = cost, sint, - , for 0st= 3 (a) Set up the integral used to evaluate the line integral using a parametric description of C. Use increasing limits of integration. ()dt (Type exact answers.) (b) Select the correct choice below and fill in the answer box(es) to complete your choice. (Type exact answers.) O A. If A is the first point on the curve, then the value of the line integral is @(A). O B. If A is the first point on the curve, and B is the last point on the curve, then the value of the line integral is q(A) - Q(B). O C. If A is the first point on the curve, and B is the last point on the curve, (), then the value of the line integral is q(B) -Q(A). O D. If B is the last point on the curve, then the value of the line integral is q(B). Using either method, [ vp. dr= . C (Type an exact answer.)Verify that the Fundamental Theorem for line integrals can be used to evaluate the following line lntegral, and then evaluate the line integral using this theorem. IV [a _x cos y] - dr, where C is the line from [0,0] to (In 11:) c Select the coned choice below and ll in the answer box to complete your choice as needed. - The Fundamental Theorem for line integrals can be used to evaluate the line integral because the function is conservative on its domain and has a potential function (pow) =D. (Type an exact answer.) O B. The fundion is not conservative on its domain, and therefore, the Fundamental Theorem for line integrals cannot be used to evaluate the line integral. IV (a q cos y] - dr = (Simplify your answer.)