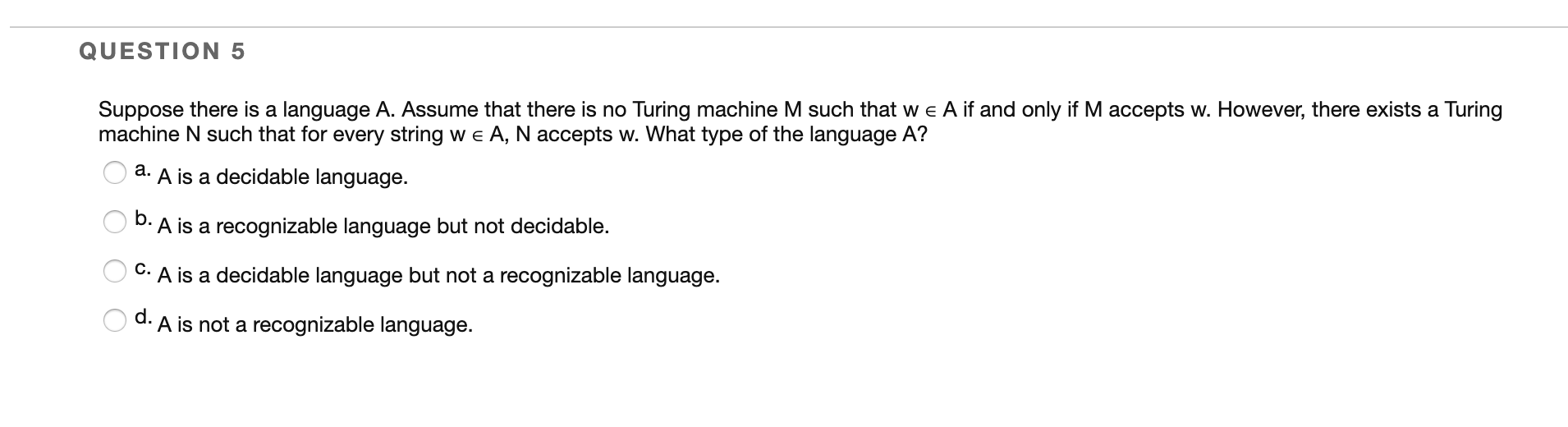
Every Turing machine will enter either accept or reject when processes an input string. True False QUESTION 2 Multi-tape Turing machine is more powerful than single-tape Turing machine. In other words, there are some problem that can only be done by a multi- tape Turing machine that cannot be done by a single-tape Turing machine. True False QUESTION 3 As in Nondeterministic Finite Automata, to trace a Nondeterministic Turing machine, we use a computational tree. In which condition when we consider a nondeterministic Turing machine accept a string? One of the branch ends up in accept At least two branches end up in accept- All of the branch end up in accept- None of the branch ends up in greject- QUESTION 5 Suppose there is a language A. Assume that there is no Turing machine M such that we A if and only if M accepts w. However, there exists a Turing machine N such that for every string we A, N accepts w. What type of the language A? O a. A is a decidable language. b. A is a recognizable language but not decidable. O C. A is a decidable language but not a recognizable language. O d. A is not a recognizable language. Every Turing machine will enter either accept or reject when processes an input string. True False QUESTION 2 Multi-tape Turing machine is more powerful than single-tape Turing machine. In other words, there are some problem that can only be done by a multi- tape Turing machine that cannot be done by a single-tape Turing machine. True False QUESTION 3 As in Nondeterministic Finite Automata, to trace a Nondeterministic Turing machine, we use a computational tree. In which condition when we consider a nondeterministic Turing machine accept a string? One of the branch ends up in accept At least two branches end up in accept- All of the branch end up in accept- None of the branch ends up in greject- QUESTION 5 Suppose there is a language A. Assume that there is no Turing machine M such that we A if and only if M accepts w. However, there exists a Turing machine N such that for every string we A, N accepts w. What type of the language A? O a. A is a decidable language. b. A is a recognizable language but not decidable. O C. A is a decidable language but not a recognizable language. O d. A is not a recognizable language