Everything is right except for the last box : f(x) has a point of inflection at each point x in this set.

I can't seem to get it.

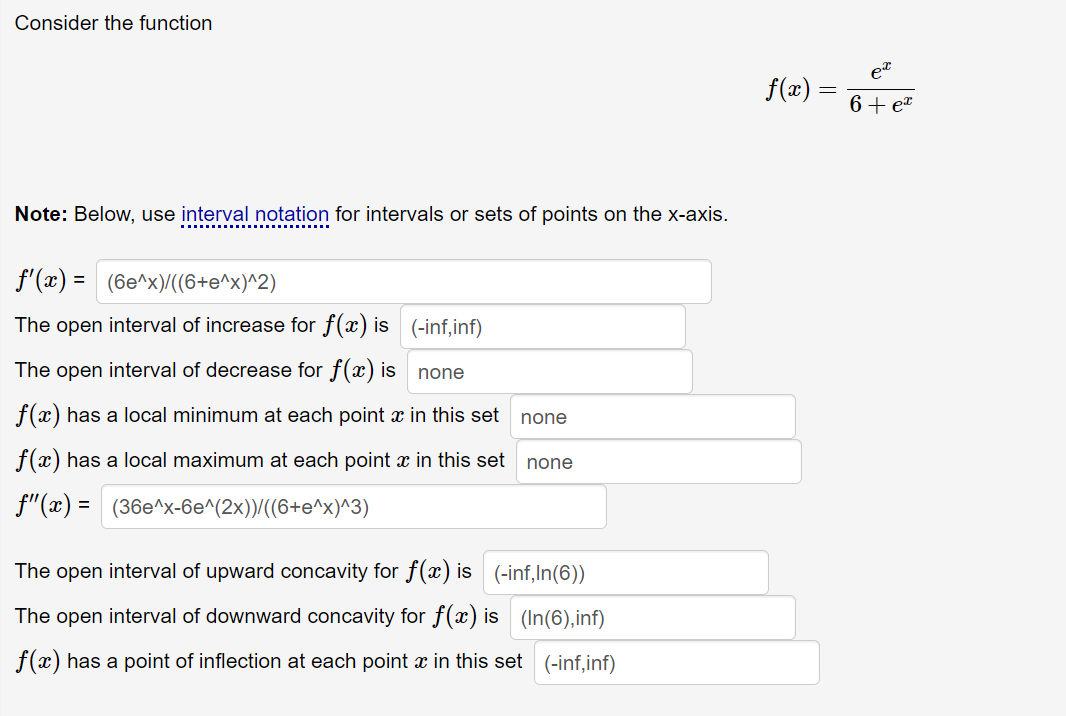
Consider the function f(a) =- 6 + er Note: Below, use interval notation for intervals or sets of points on the x-axis. f'(a) = (6ex)/((6+e^x)^2) The open interval of increase for f(x) is (-inf,inf) The open interval of decrease for f(x) is none f(a) has a local minimum at each point a in this set none f (a) has a local maximum at each point a in this set none f"(a) = (36ex-6e^(2x))/((6+e^x)^3) The open interval of upward concavity for f (x) is (-inf,In(6)) The open interval of downward concavity for f(a) is (In(6), inf) f (ac) has a point of inflection at each point a in this set (-inf,inf)