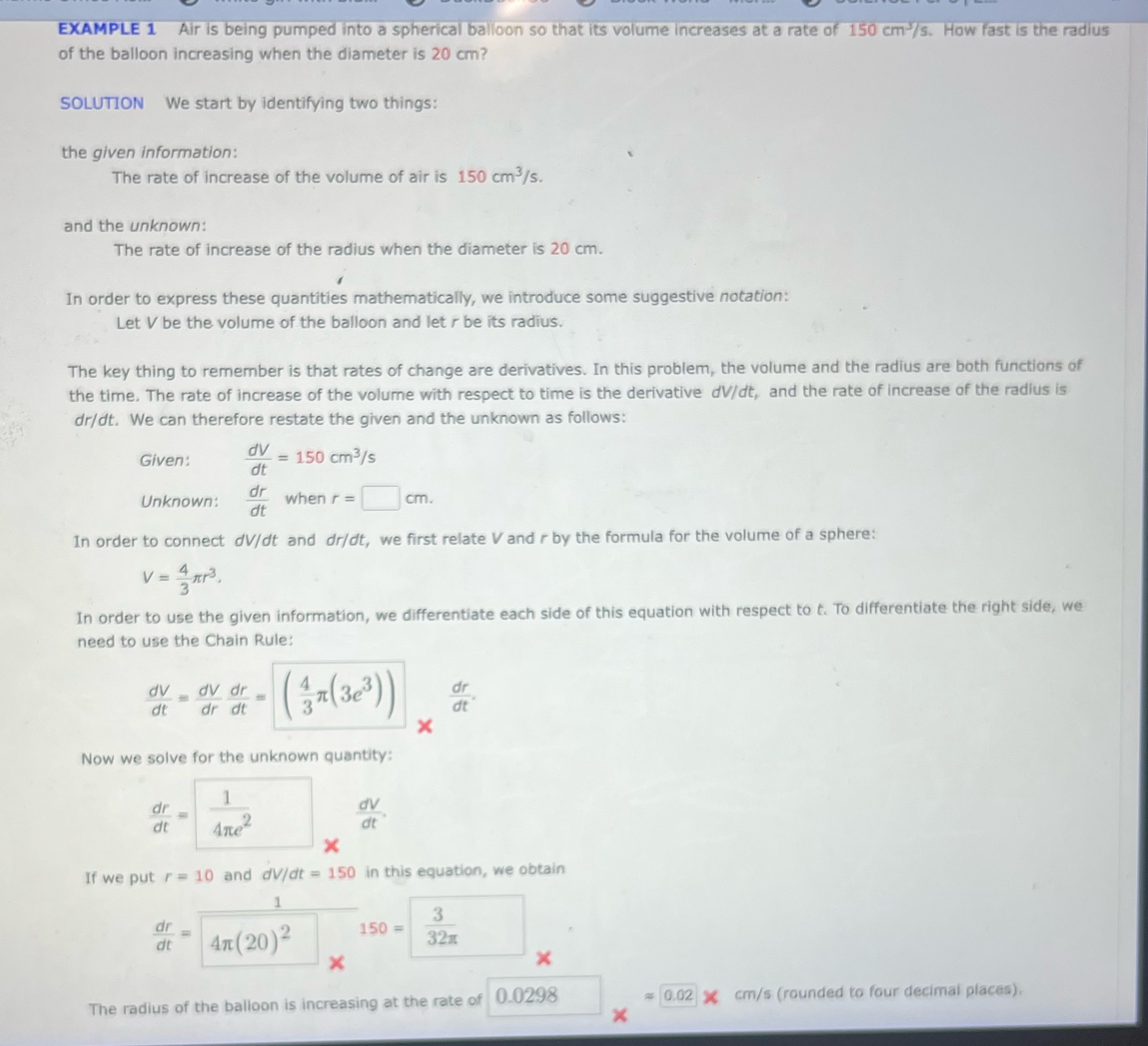
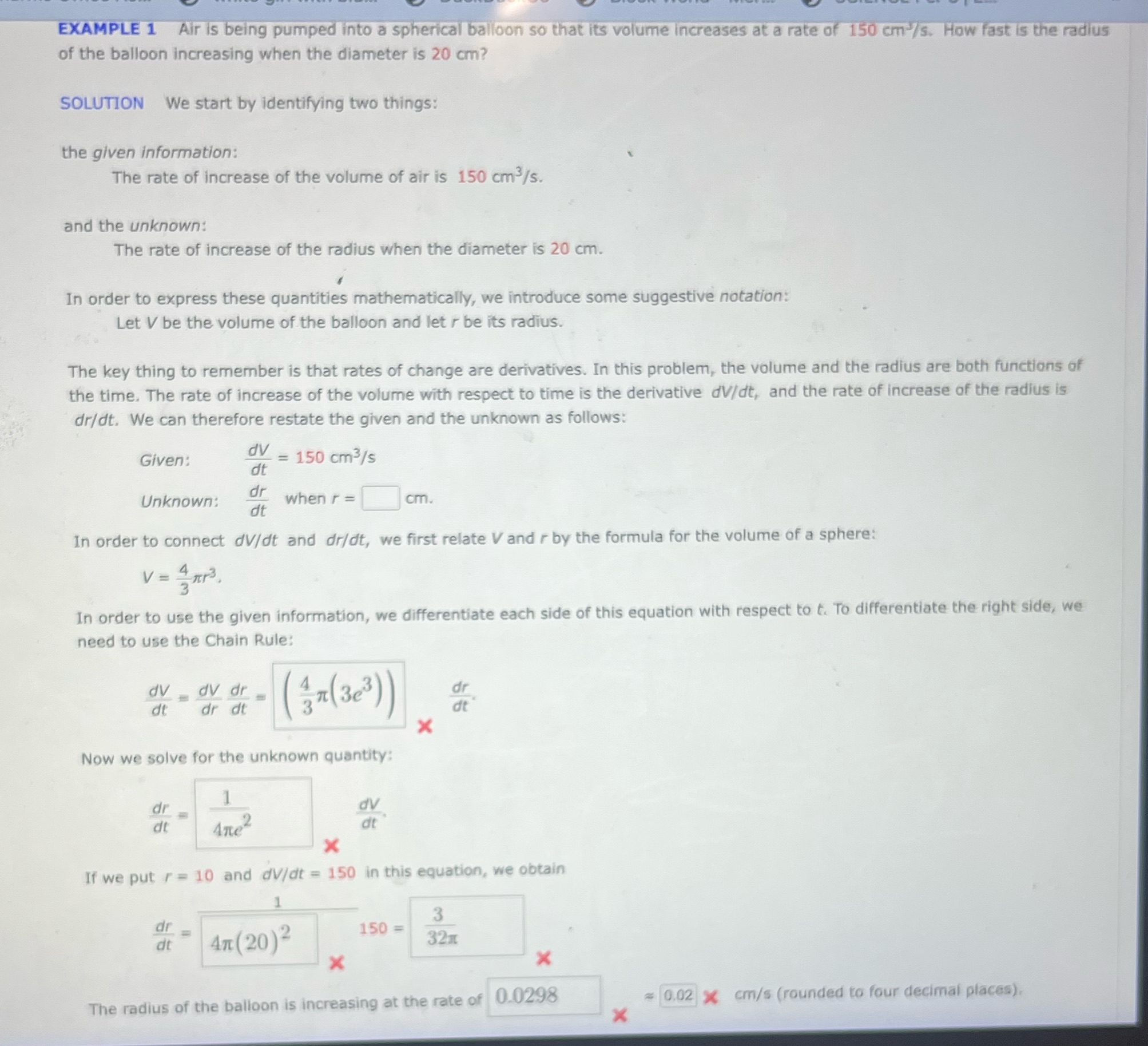
EXAMPLE 1 Air is being pumped into a spherical balloon so that its volume increases at a rate of 150 cm /s. How fast is the radius of the balloon increasing when the diameter is 20 cm? SOLUTION We start by identifying two things: the given information: The rate of increase of the volume of air is 150 cm3/s. and the unknown: The rate of increase of the radius when the diameter is 20 cm. In order to express these quantities mathematically, we introduce some suggestive notation: Let V be the volume of the balloon and let r be its radius. The key thing to remember is that rates of change are derivatives. In this problem, the volume and the radius are both functions of the time. The rate of increase of the volume with respect to time is the derivative dV/dt, and the rate of increase of the radius is dr/dt. We can therefore restate the given and the unknown as follows: Given: dy = 150 cm3/s dt Unknown: dr dt when r = cm. In order to connect dV/dt and dr/dt, we first relate V and r by the formula for the volume of a sphere: V = 4 mr3 In order to use the given information, we differentiate each side of this equation with respect to t. To differentiate the right side, we need to use the Chain Rule: dv dv dr dr dt dr dt dt X Now we solve for the unknown quantity: dv Are2 at X If we put r = 10 and dV/dt = 150 in this equation, we obtain 3 dr 150 = dt 47 (20)2 X X The radius of the balloon is increasing at the rate of 0.0298 = 0.02 x cm/s (rounded to four decimal places). X