Question: Example # 1: Determine the point(s) of intersection of each line and plane, if possible. a) L1: [x,y,z]=[4,2,6]+t[1,-2,3] andjr] : 13x+7y2216=0 264 3/ 2+1 b)
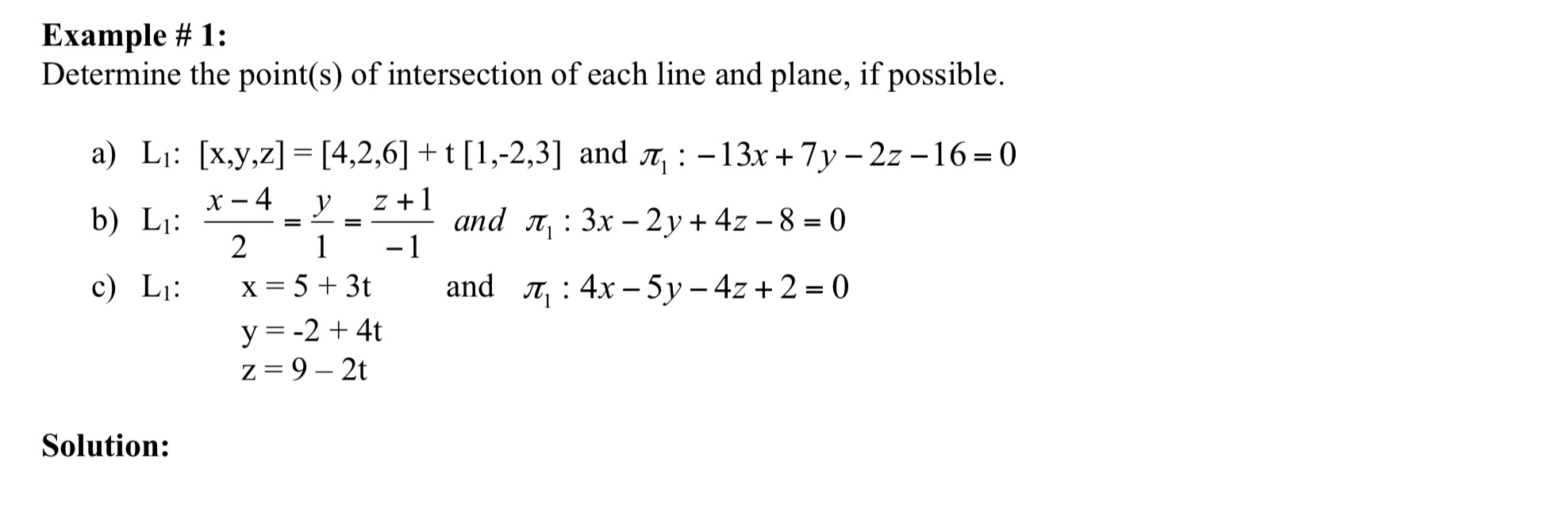
![and plane, if possible. a) L1: [x,y,z]=[4,2,6]+t[1,-2,3] andjr] : 13x+7y2216=0 264 3/](https://s3.amazonaws.com/si.experts.images/answers/2024/07/668c342f5f4eb_431668c342f2dfc1.jpg)
Example # 1: Determine the point(s) of intersection of each line and plane, if possible. a) L1: [x,y,z]=[4,2,6]+t[1,-2,3] andjr] : 13x+7y2216=0 264 3/ 2+1 b) L1: T_l=1 and zlz3x2y+4z8=0 0) L1: x=5+3t and m:4x5y4z+2=0 y=-2+4t z=92t Solution: Skew lines are lines in three dimensions that are not parallel and do not intersect. Two skew lines may lie in parallel planes. To show that lines are skew lines; Example # 1: Show that L1 and L2 are skew lines. L1 =y_-2=z_-1 and L2; x_-1=y_+3=5 3 1 1 2 1 1 Solution
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


