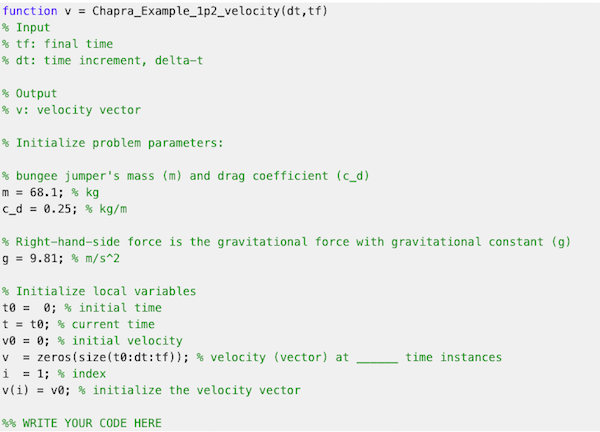
Example 1.2. Perform the same computation as Example 1.1 (below and in chapter 1 of the textbook), but use Eq. (1.12), v (ti+1) = v(t))+ 8 [8 - 0(13] (t+1 4) to compute velocity (downward speed) with Euler's method. Employ a step size of 2 seconds for the calculation. Write MATLAB code that can handle other step sizes. Example 1.1. A bungee jumper with a mass of 68.1 kg leaps from a stationary hot air balloon. Use Eq. (1.9) to compute velocity for the first 12 s of free fall. Also determine the terminal velocity that will be attained for an infinitely long cord (or alternatively, the jumpmaster is having a particularly bad day!). Use a drag coefficient of 0.25 kg/m function v = Chapra_Example_1p2_velocity(dt,tf) % Input % tf: final time % dt: time increment, delta-t % Output % V: velocity vector % Initialize problem parameters: % bungee jumper's mass (m) and drag coefficient (c_d) m = 68.1; % kg c_d = 0.25; % kg/m % Right-hand-side force is the gravitational force with gravitational constant (g) 9 = 9.81; % m/s^2 % Initialize local variables to = 0; % initial time t = t0; % current time v0 = ; % initial velocity = zeros(size(t:dt:tf)); % velocity (vector) at i = 1; % index v(i) = vo; % initialize the velocity vector V time instances %% WRITE YOUR CODE HERE