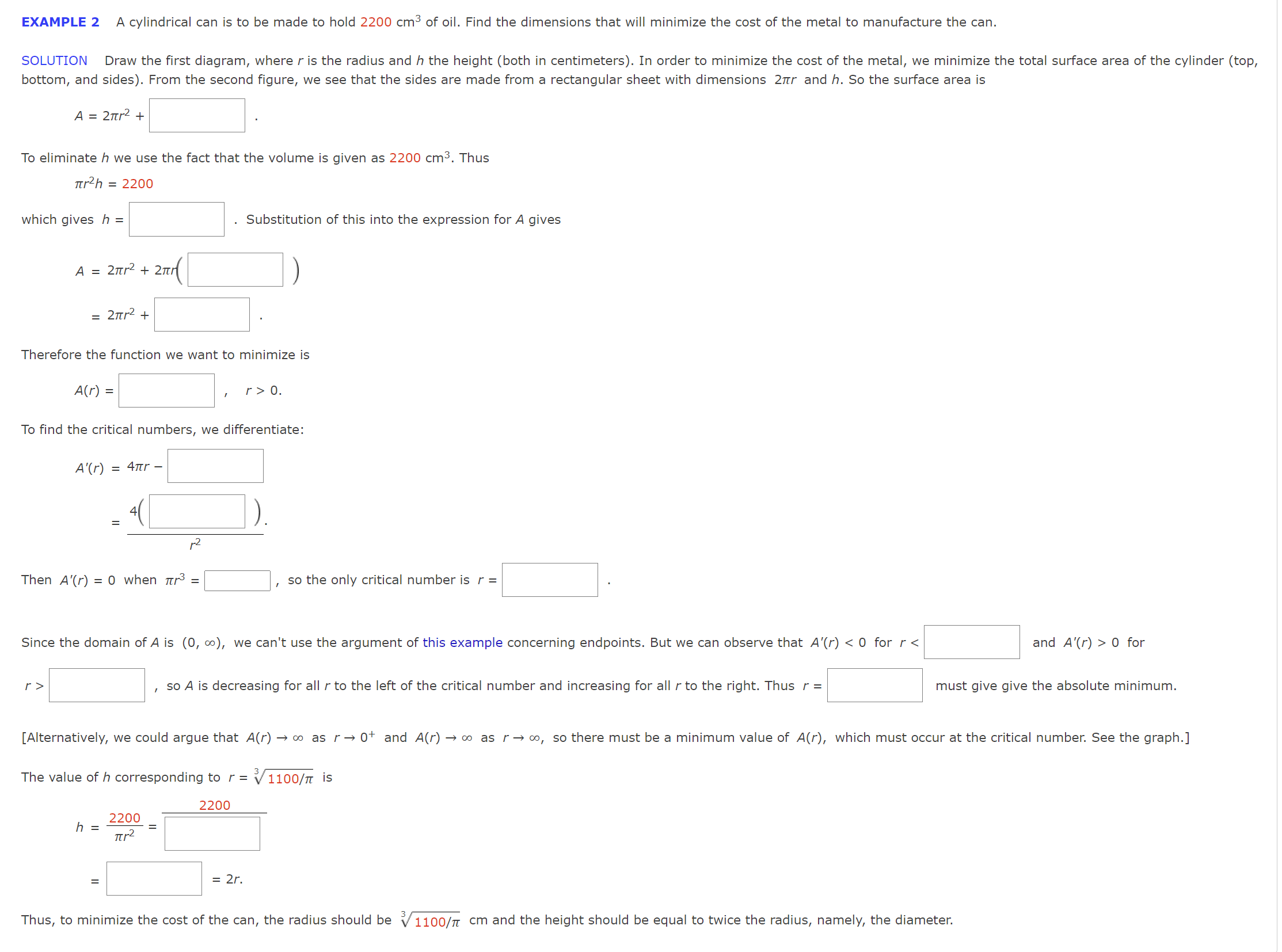
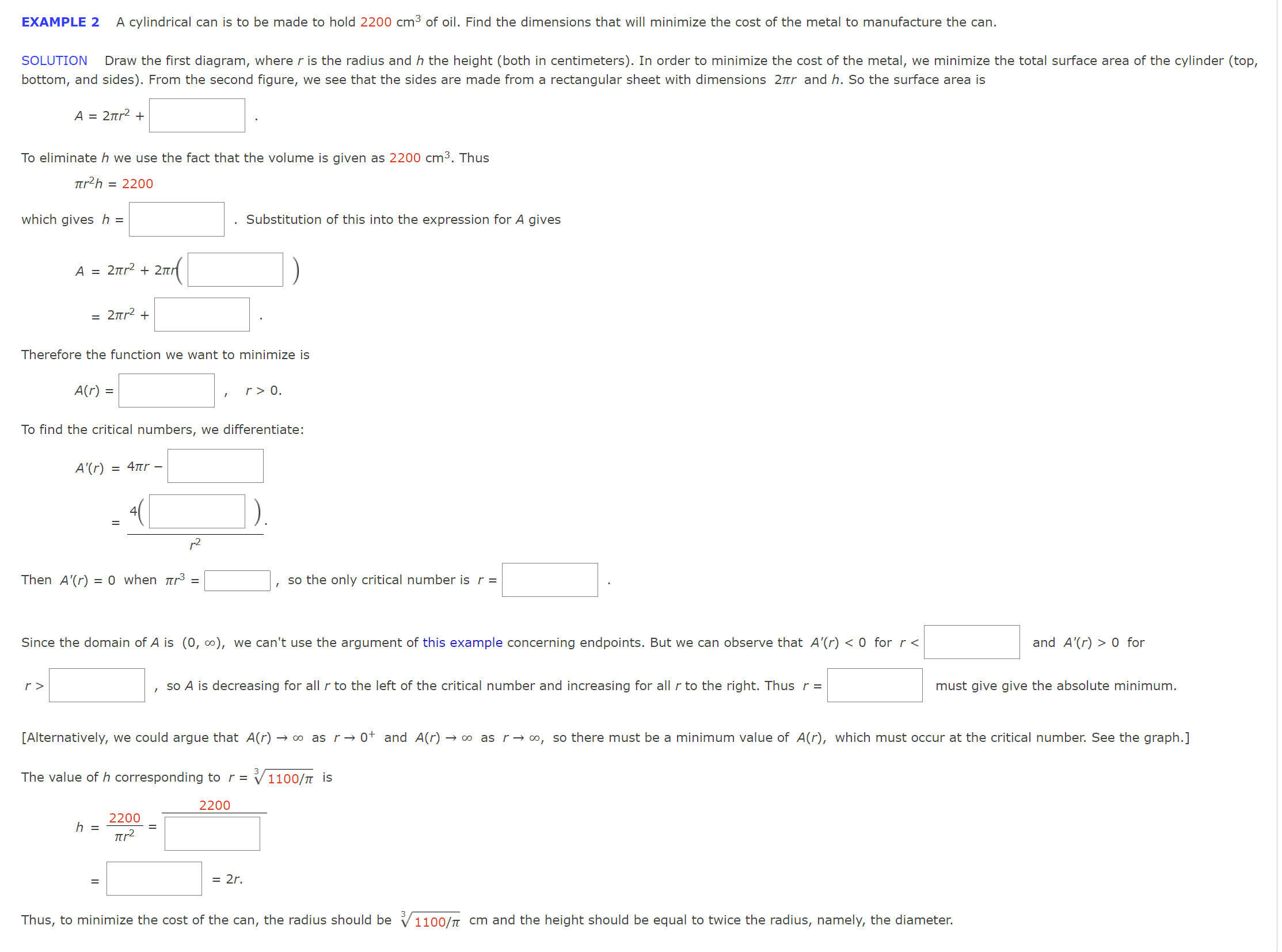
EXAMPLE 2 A cylindrical can is to be made to hold 2200 cm3 of oil. Find the dimensions that will minimize the cost of the metal to manufacture the can. SOLUTION Draw he rst diagram, where r is the radius and h the height (both in centimeters). In order to minimize the cost of the metal, we minimize the total surface area of the cylinder (top, bottom, and sides). From the second gure, we see that the sides are made from a rectangular sheet with dimensions 2111' and h. So the surface area is A=2nr2+ To eliminate h we use the fact that the volume is given as 2200 cm3. Thus mlh = 2200 which gives h = . Substitution of this into the expression forA gives A = 2117'2 + 211r( ) = 21'rr2 + Therefore the function we want to minimize is A(r) = , r>O. To find the critical numners, we differentiate: A'(r) = 41'L'r - 4( ). r2 Then A'(r) = 0 when m3 = E , so the only critical number is r = Since the domain ofA is (0, 00), we can't use the argument of this example concerning endpoints. But we can observe that A'(r) 0 for r > , so A is decreasing for all r to the left of the critical number and increasing for all rto the right. Thus r = must give give the absolute minimum. [Alternatively, we could argue that A(r) > so as r) 0+ and A(r) > on as r > 00, so there must be a minimum value of A(r), which must occur at the critical number. See the graph.] The value of h corresponding to r = 3\\/ 1100/11 is 2200 2200 7'er = = 2r. Thus, to minimize the cost 0 the can, the radius should be 3\\/ 1100/11 cm and the height should be equal to twice the radius, namely, the diameter