Example file:

How to use mathlab to code this?

THis is from INTRODUCTION TO OPTIMUM DESIGN.

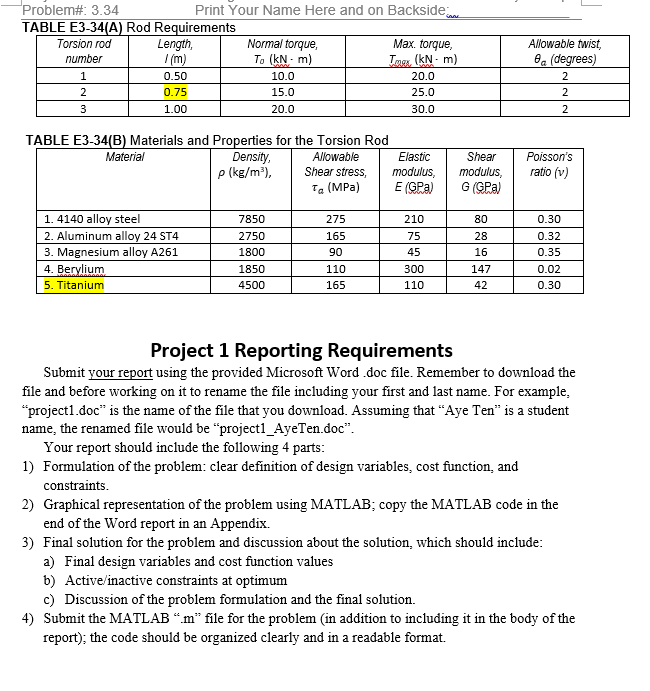
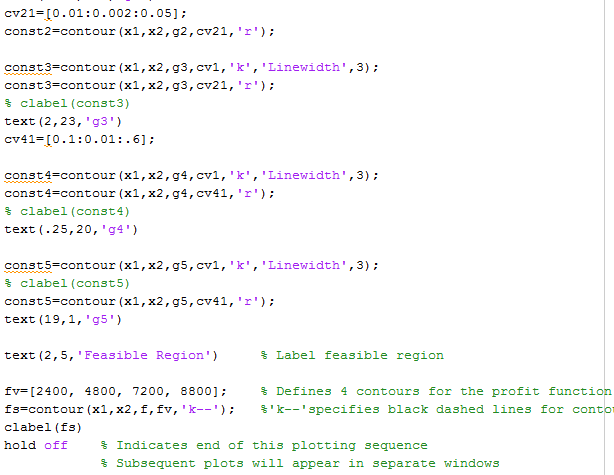
Problem# 3.34 Print Your Name Here and on Backside esign a hollow torsion rod shown in Fig.E3.34 to satisfy the following: I. The calculated shear stress, 1 shall not exceed the allowable shear stress Tunder the normal operation torque To (N-m) 2. The calculated angle of twist, | shall not exceed the allowable twist, (radians) 3. The member shall not buckle under a short duration torque of Tag (N-m) Requirements for the rod and material properties are given in Table E3.34 A) and E3.34(B) (use length 0.75m and Titanium material). Use the following design variables: x outside diameter of the shaft; x2 ratio of inside/outside diameter, di/ do. Formulate the design optimization problem, and using graphical optimization, determine the inside and outside diameters for a minimum mass rod to meet the above design requirements. Compare the hollow rod with an equivalent solid rod (di/do-0). Use consistent set of units (e.g, Newtons and millimeters) and let the minimum and maximum values for design variables be given as 0.02 s do S 0.5 m. 0.60 Ss 0.999 Useful expressions for the rod are: Mass of rod: Calculated shear stress: Calculated angle of twist: Critical buckling torque: 4 --To, radians GJ 2.5 12V2(1-v*)0.75 d Notation M mass of the rod (kg) do- outside diameter of the rod (m) di inside diameter of the rod (m) Torque mass density of material (kg/m2 l= length of the rod (m) To: Normal operation torque (Nm) c Distance from rod axis to extreme fiber (m) J-Polar moment of inertia (m4); A = Cross-sectional area (m2)--( d -d 6Angle of twist (radians) G Modulus of rigidity (Pa) Ter-Critical buckling torque (Nm) E = Modulus of elasticity (Pa) v = Poisson's ratio (4-d) ?) d, FIGURE E3-34 Hollow torsion rod Problem# 3.34 Print Your Name Here and on Backside esign a hollow torsion rod shown in Fig.E3.34 to satisfy the following: I. The calculated shear stress, 1 shall not exceed the allowable shear stress Tunder the normal operation torque To (N-m) 2. The calculated angle of twist, | shall not exceed the allowable twist, (radians) 3. The member shall not buckle under a short duration torque of Tag (N-m) Requirements for the rod and material properties are given in Table E3.34 A) and E3.34(B) (use length 0.75m and Titanium material). Use the following design variables: x outside diameter of the shaft; x2 ratio of inside/outside diameter, di/ do. Formulate the design optimization problem, and using graphical optimization, determine the inside and outside diameters for a minimum mass rod to meet the above design requirements. Compare the hollow rod with an equivalent solid rod (di/do-0). Use consistent set of units (e.g, Newtons and millimeters) and let the minimum and maximum values for design variables be given as 0.02 s do S 0.5 m. 0.60 Ss 0.999 Useful expressions for the rod are: Mass of rod: Calculated shear stress: Calculated angle of twist: Critical buckling torque: 4 --To, radians GJ 2.5 12V2(1-v*)0.75 d Notation M mass of the rod (kg) do- outside diameter of the rod (m) di inside diameter of the rod (m) Torque mass density of material (kg/m2 l= length of the rod (m) To: Normal operation torque (Nm) c Distance from rod axis to extreme fiber (m) J-Polar moment of inertia (m4); A = Cross-sectional area (m2)--( d -d 6Angle of twist (radians) G Modulus of rigidity (Pa) Ter-Critical buckling torque (Nm) E = Modulus of elasticity (Pa) v = Poisson's ratio (4-d) ?) d, FIGURE E3-34 Hollow torsion rod