Question: Example (ref text 6-1 #6) . Find the area between y = In(x), y = =, and the lines x = 1 and x =

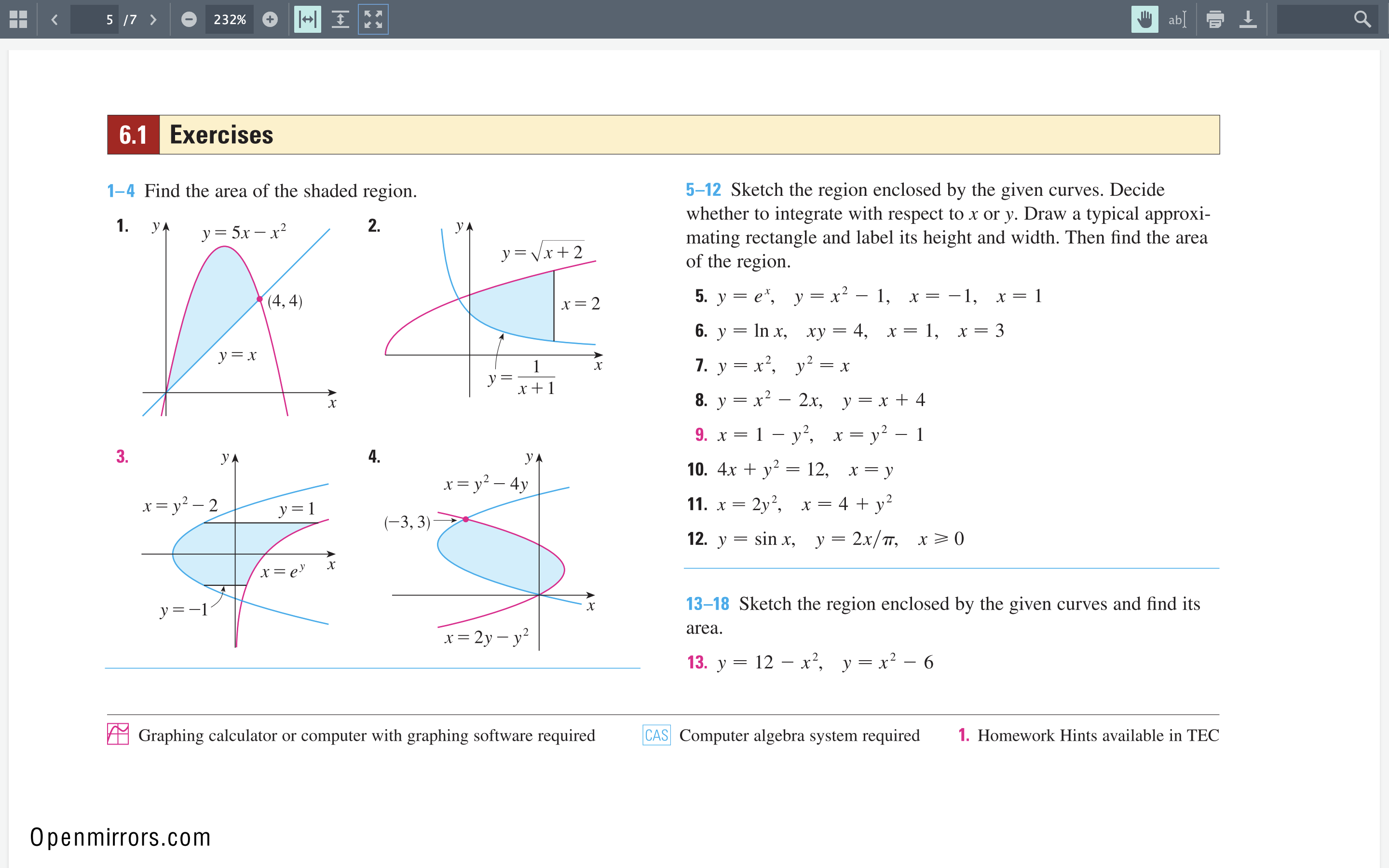

![] dx O y = In(x) Area = S [# - In(x)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664ffc73200c_1116664ffc718c25.jpg)
![] dx Area = [4In(x) - (xIn(x) - x) ], The antiderivative](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664ffc792a4f_1116664ffc76b917.jpg)
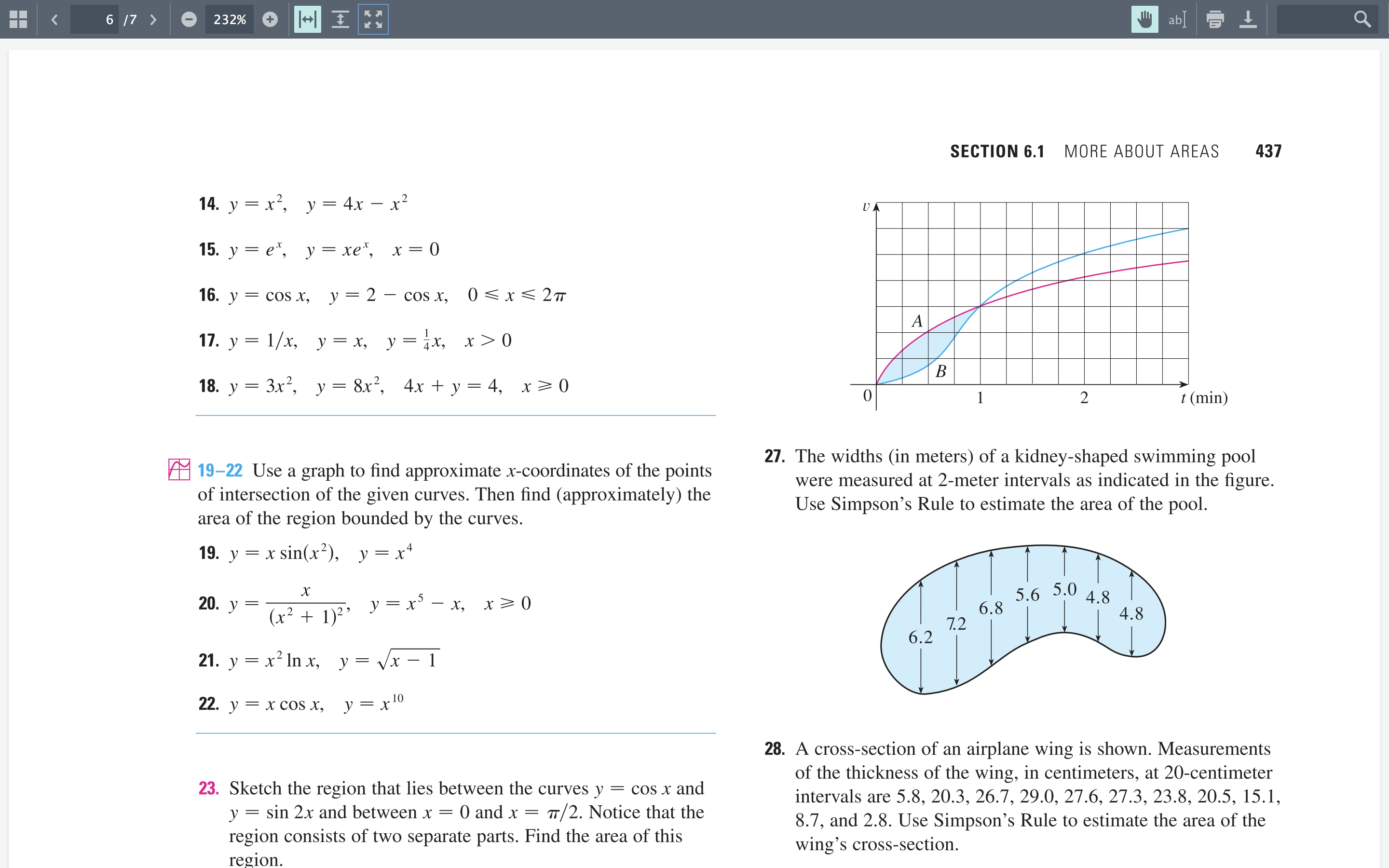
Example (ref text 6-1 #6) . Find the area between y = In(x), y = =, and the lines x = 1 and x = 3. Tip: Always draw the graphs on your paper to visualize the area y = 4/x Area = S [Top - Bottom ] dx O y = In(x) Area = S [# - In(x) ] dx Area = [4In(x) - (xIn(x) - x) ], The antiderivative of In(x) is found by integrating by parts Area = [4In(3) - (3 In(3) - 3)] - [4In(1) - (1In(1) - 1) ] Area = In(3) + 25 17 > 232% + 1+1 I ab 6.1 Exercises 1-4 Find the area of the shaded region. 5-12 Sketch the region enclosed by the given curves. Decide 1. YA y = 5x - x2 2. YA whether to integrate with respect to x or y. Draw a typical approxi- y = Vx+ 2 mating rectangle and label its height and width. Then find the area of the region. ( 4, 4 ) x = 2 5. y = el, y = x2 - 1, x = -1, x=1 6. y = Inx, xy = 4, x = 1, x=3 y =x y= - 7. y = x2, yz = x x+1 8. y = x2 - 2x, y = x+4 9. x = 1 -y', x=y2 - 1 3. YA 4. YA x= y2 - 4y 10. 4x + y2 = 12, x =y x=y2 - 2 y =1 11. x = 2y?, x = 4+ 2 (-3, 3) 12. y = sin x, y = 2x/7, x20 x = ey y = -1- 13-18 Sketch the region enclosed by the given curves and find its x = 2y -yz area. 13. y = 12 - x, y = x2 - 6 Graphing calculator or computer with graphing software required CAS Computer algebra system required 1. Homework Hints available in TEC Openmirrors.com14.y:x2, 51:4)cx2 15.y=e', y=xe', x=0 16.y=cosx, y=27cosx, OSxS277 17.y=l/x, y=x, y=%x, x>0 18.y=3x2, y=8x2, 4x+y=4, x20 W 1922 Use a graph to nd approximate xcoordinates of the points of intersection of the given curves. Then nd (approximately) the area of the region bounded by the curves. 19. y = x sin(x2), y = x4 L (x2 + 1)?' 21. y=x21nx, y=x/x1 22. y=xcosx, y=x10 20.y= y=x5x, x20 23. Sketch the region that lies between the curves y : cos x and y = sin 2x and between x = 0 and x = 7r/ 2. Notice that the region consists of two separate parts. Find the area of this region. SECTION 6.1 MORE ABOUT AREAS 437 A/// 18 , 0 1 2 t (min) 27. The widths (in meters) of a kidneyshaped swimming pool were measured at 2meter intervals as indicated in the gure. Use Simpson's Rule to estimate the area of the pool. 28. A crosssection of an airplane wing is shown. Measurements of the thickness of the wing, in centimeters, at 20centimeter intervals are 5.8, 20.3, 26.7, 29.0, 27.6, 27.3, 23.8, 20.5, 15.1, 8.7, and 2.8. Use Simpson's Rule to estimate the area of the wing's cross
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


