example that they were mentioned :

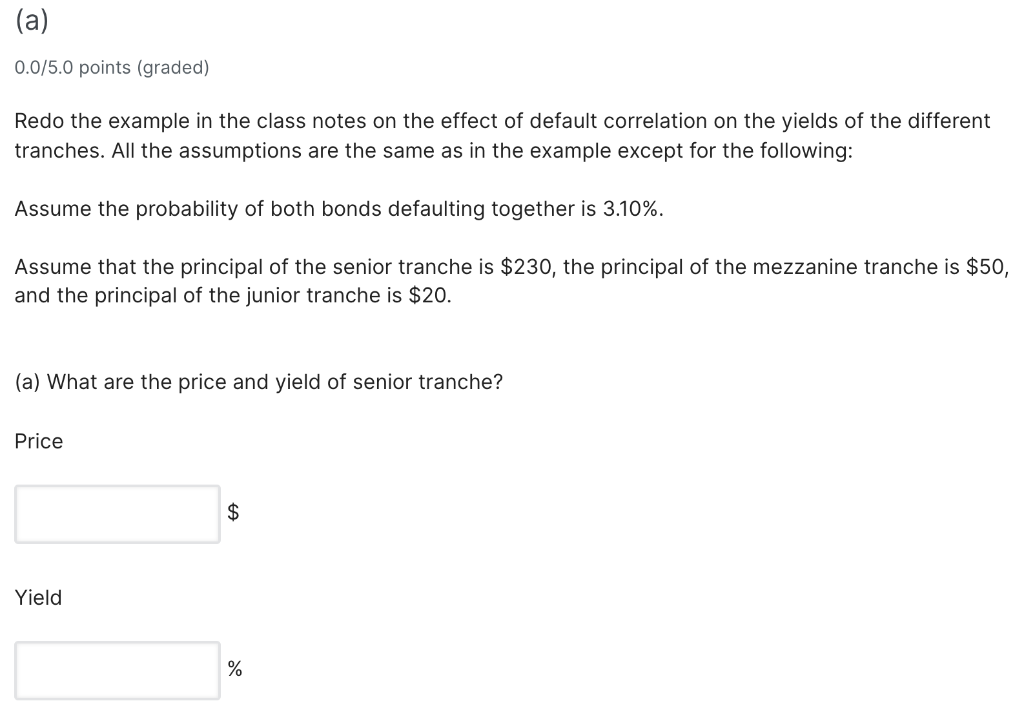
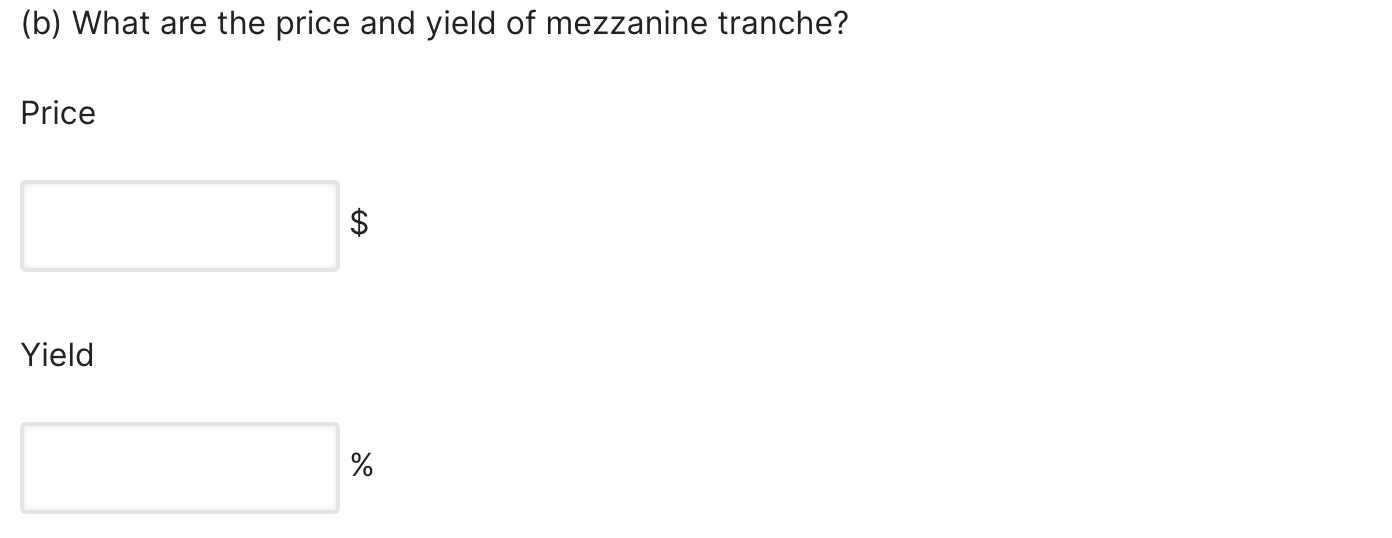
(a) 0.0/5.0 points (graded) Redo the example in the class notes on the effect of default correlation on the yields of the different tranches. All the assumptions are the same as in the example except for the following: Assume the probability of both bonds defaulting together is 3.10%. Assume that the principal of the senior tranche is $230, the principal of the mezzanine tranche is $50, and the principal of the junior tranche is $20. (a) What are the price and yield of senior tranche? Price $ Yield % (b) What are the price and yield of mezzanine tranche? Price $ Yield % (c) What are the price and yield of junior tranche? Price $ Yield % Example: Effects of default correlation on value Consider a simple CDO based on two notes o Note: probabilities are risk neutral so that price is found discounting expected discounted cash flow at risk-free rate. Both notes are zero-coupon and have one-year maturities: Note 1: $100 principal; 50% expected recovery rate (or $50); price = $95 Note 2: $200 principal; 40% expected recovery rate (or $80); price = $179.5 = Assuming the one-year LIBOR rate is 2 percent, then the (risk-neutral) probability of default, pi, for each note i is: 1 Note 1: ($50 p1 + $100(1 P)) = $953 P1 = 6.2% 1.02 Note 2: 1 +($80p2 +$200(1 P2)) = $179.5= P2 = 14.1% 1.02 = Example continued Assume that the probability of both notes defaulting at the same time is 1 percent: The probability of only note 1 defaulting is 5.2 percent (6.2 1), The probability of only note 2 defaulting is 13.1 percent (14.1 1), The probability of neither note defaulting is 80.7 percent (100 (13.1 + 5.2 + 1)). - O - Note 2 Note Assume the $300 CDO is divided into three tranches: the senior tranche ($220 of principal), the mezzanine tranche ($60 of principal), the junior tranche ($20 principal). 13.1% 1%) 5.2% For each tranche, the expected payouts under each default scenario can be calculated. (a) 0.0/5.0 points (graded) Redo the example in the class notes on the effect of default correlation on the yields of the different tranches. All the assumptions are the same as in the example except for the following: Assume the probability of both bonds defaulting together is 3.10%. Assume that the principal of the senior tranche is $230, the principal of the mezzanine tranche is $50, and the principal of the junior tranche is $20. (a) What are the price and yield of senior tranche? Price $ Yield % (b) What are the price and yield of mezzanine tranche? Price $ Yield % (c) What are the price and yield of junior tranche? Price $ Yield % Example: Effects of default correlation on value Consider a simple CDO based on two notes o Note: probabilities are risk neutral so that price is found discounting expected discounted cash flow at risk-free rate. Both notes are zero-coupon and have one-year maturities: Note 1: $100 principal; 50% expected recovery rate (or $50); price = $95 Note 2: $200 principal; 40% expected recovery rate (or $80); price = $179.5 = Assuming the one-year LIBOR rate is 2 percent, then the (risk-neutral) probability of default, pi, for each note i is: 1 Note 1: ($50 p1 + $100(1 P)) = $953 P1 = 6.2% 1.02 Note 2: 1 +($80p2 +$200(1 P2)) = $179.5= P2 = 14.1% 1.02 = Example continued Assume that the probability of both notes defaulting at the same time is 1 percent: The probability of only note 1 defaulting is 5.2 percent (6.2 1), The probability of only note 2 defaulting is 13.1 percent (14.1 1), The probability of neither note defaulting is 80.7 percent (100 (13.1 + 5.2 + 1)). - O - Note 2 Note Assume the $300 CDO is divided into three tranches: the senior tranche ($220 of principal), the mezzanine tranche ($60 of principal), the junior tranche ($20 principal). 13.1% 1%) 5.2% For each tranche, the expected payouts under each default scenario can be calculated