Question: Exercise 1: Polynomial Arithmetic for GF(4) Develop a set of tables similar to Table 5.3 shown below, for GF(4) with Modulo (x2 + x +
Exercise 1: Polynomial Arithmetic for GF(4) Develop a set of tables similar to Table 5.3 shown below, for GF(4) with Modulo (x2 + x + 1).
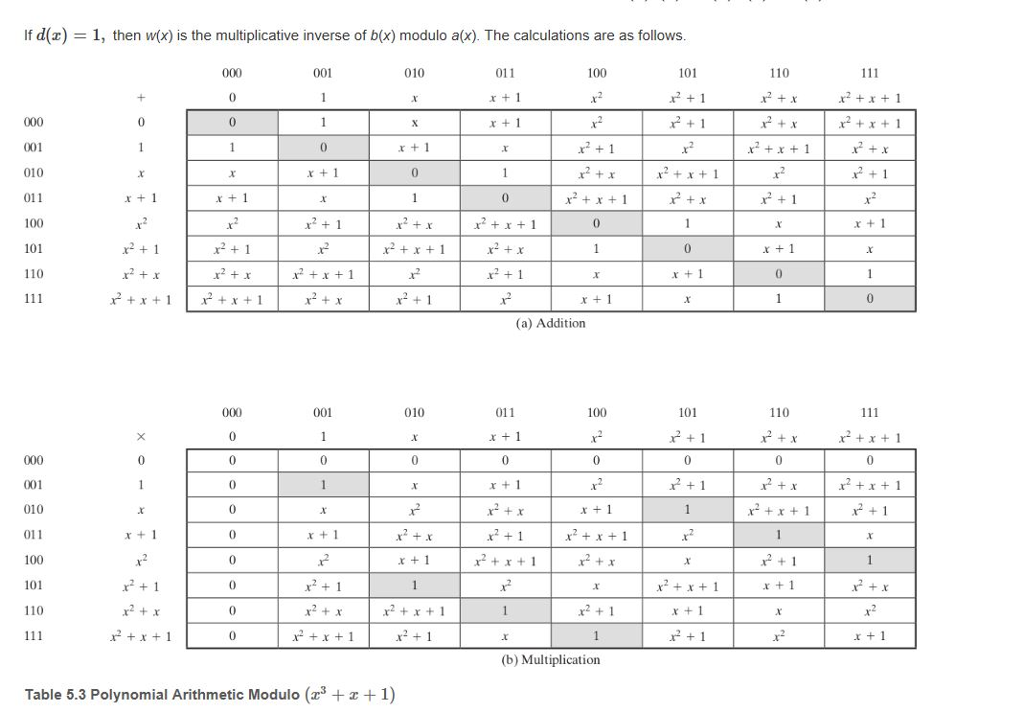
If d(z) 1, then w(x) is the multiplicative inverse of b(x) modulo a(x). The calculations are as follows 001 010 101 011 x 1 x+ 1 100 110 2+x1 r2+x1 001 010 011 100 101 110 r +1 2x 1 +x r +1 r + 1 x2+x1 2x x2+x1 r2+x+ 1 r 1 r2x1 r +1 x1 x +1 (a) Addition 001 010 011 100 101 110 x + 1 2 +a+1 001 010 011 100 101 110 r+1 x2x1 r+ 1 xx 1 t +1 x2+x1 xx+1 x +1 r2+x r2x r2x1 x + 1 r+x+1 t+ 1 (b) Multiplication Table 5.3 Polynomial Arithmetic Modulo (z+1)
Step by Step Solution
There are 3 Steps involved in it
To develop similar tables for G F 4 G F 4 using modulo x 2 x 1 x 2 x 1 we need to define the elements and perform polynomial addition and multiplication operations in this field Elements of GF4 G F 4 G F 4 has four elements 0 1 and 1 1 where is a root of the irreducible polynomial x 2 x 1 x 2 x 1 In this field 2 1 2 1 3 1 3 1 Addition Table for GF4 Addition in G F 4 G F 4 is done modulo 2 binary addition 0 1 1 0 0 1 1 1 1 0 1 1 0 1 1 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 1 1 1 1 0 Multiplication Table for GF4 Multiplication follows the rules of modular arithmetic with x 2 x 1 x 2 x 1 0 1 1 0 0 0 0 0 1 0 1 1 0 1 1 1 0 1 1 0 1 1 0 0 0 0 0 1 0 1 1 0 1 1 1 0 1 1 Explanation of the Calculations Addition Addition is straightforward binary addition modulo 2 Multiplication Any element multiplied by 0 is 0 Any element multiplied by 1 is the element ... View full answer

Get step-by-step solutions from verified subject matter experts


