Question: Exercise 1.9. Let R be a ring, and let N = nilrad( R) be the nilradical of R. Show that the following are equivalent. (1)

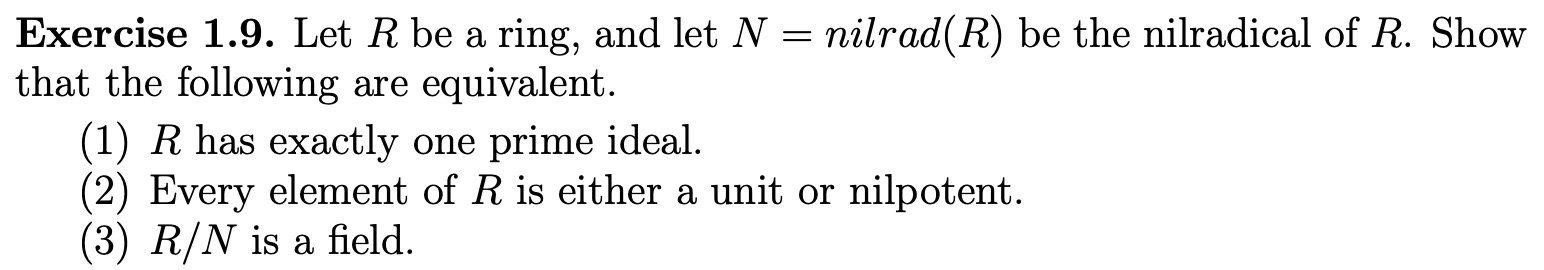
Exercise 1.9. Let R be a ring, and let N = nilrad( R) be the nilradical of R. Show that the following are equivalent. (1) R has exactly one prime ideal. (2) Every element of R is either a unit or nilpotent. (3) R/N is a field

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

the belw (b) Compare and contrast the struct and union keywords in C, supplying an example of a situation where it would be more appropriate to use a union rather than a struct. (c) Explain the...

Exercise 5 Three dice are tossed, one red, one blue, and one green. a. What is the probability that the sum of the three faces showing equals 7? b. Write an R program that simulates this random...

9/14/10 12:39 PM Page 381 Chapter dug84356_ch06a.qxd 6 Rational Expressions Advanced technical developments have made sports equipment faster, lighter, and more responsive to the human body. Behind...

if do - a, + a2 - . . . (-1)*a, is divisible by 11. 33. Show that the number 7, 176,825,942, 116,027,211 is divisible by 9 but not divisible by 11. 34. Show that the number 9,897,654,527,609,805 is...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

1 Due September 6 Problems 1.20, 1.26, 1.30 from the textbook Add-on sketch of a proof of existence of a set which is not Lebesgue-measurable. The original example is due to G. Vitali. Let = [0, 1);...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

How we proceed f(1). Find a polynomial g(x) in Z[x] such that Ker d = (g(x)). Is there more than one possibility for g(x)? To what familiar ring is Z[x]/Ker o isomorphic? Do this exercise with Z...

An electron gun with its collector at a potential of 100 V fires out electrons in a spherical bulb containing hydrogen gas at low pressure (~102 mm of Hg). A magnetic field of 2.83 x 10 T curves the...

A particle of mass m is subject to a force F(t) = mebt. The initial position and speed are zero. Find x(t).

discuss how the following indivduals would be affected by inflation of 9 percent per year: a . a student who is heavily indebted with loans

A company is preparing completing their Cash Budget. The following data has been prepared for cash receipts and payments. January February March Cash receipts $1,061,200 $1,182,400 $1,091,700 Cash...