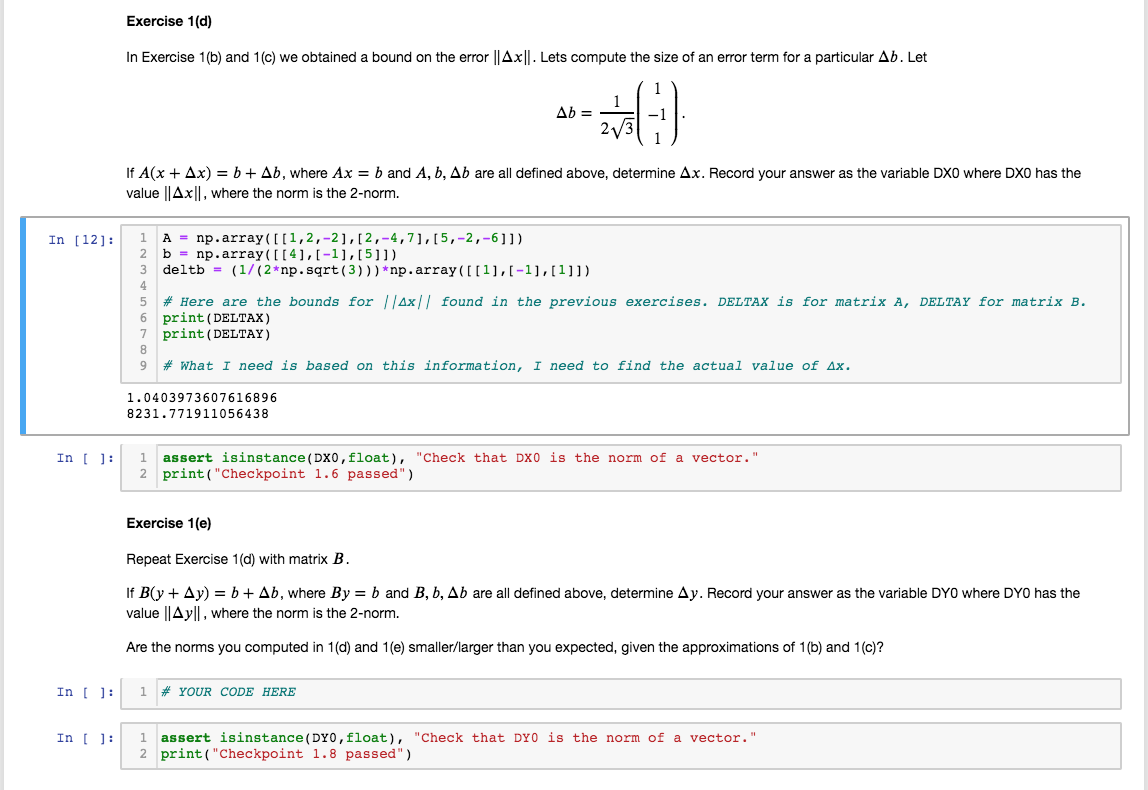
Exercise 1(d) In Exercise 1(b) and 1(c) we obtained a bound on the error ||AX||. Lets compute the size of an error term for a particular Ab. Let 1 Ab= 23 If A(x + Ax) = b + Ab, where Ax = b and A, b, Ab are all defined above, determine Ax. Record your answer as the variable DXO where DXO has the value ||AX||, where the norm is the 2-norm. In [12]: 1 2 A = np.array([[1,2,-2],[2,-4,7],[5,-2,-6]]) b = np.array([[4],[-1],[5]]) deltb = (1/(2*np.sqrt(3)))*np.array([[1],[-1],[1]]) # Here are the bounds for //x// found in the previous exercises. DELTAX is for matrix A, DELTAY for matrix B. print (DELTAX) print (DELTAY) 8 9 # What I need is based on this information, I need to find the actual value of Ax. 1.0403973607616896 8231.771911056438 In [ ]: 1 assert isinstance (Dx0, float), "Check that DxO is the norm of a vector." 2 print("Checkpoint 1.6 passed") Exercise 1(e) Repeat Exercise 1(d) with matrix B. If B(y + Ay) = b + Ab, where By = b and B, b, Ab are all defined above, determine Ay. Record your answer as the variable DYO where DYO has the value ||4y|l, where the norm is the 2-norm. Are the norms you computed in 1(d) and 1(e) smaller/larger than you expected, given the approximations of 1(b) and 1(c)? In [ ]: 1 # YOUR CODE HERE In [ ]: i assert isinstance (DYO, float), "Check that DYO is the norm of a vector." 2 print("Checkpoint 1.8 passed") Exercise 1(d) In Exercise 1(b) and 1(c) we obtained a bound on the error ||AX||. Lets compute the size of an error term for a particular Ab. Let 1 Ab= 23 If A(x + Ax) = b + Ab, where Ax = b and A, b, Ab are all defined above, determine Ax. Record your answer as the variable DXO where DXO has the value ||AX||, where the norm is the 2-norm. In [12]: 1 2 A = np.array([[1,2,-2],[2,-4,7],[5,-2,-6]]) b = np.array([[4],[-1],[5]]) deltb = (1/(2*np.sqrt(3)))*np.array([[1],[-1],[1]]) # Here are the bounds for //x// found in the previous exercises. DELTAX is for matrix A, DELTAY for matrix B. print (DELTAX) print (DELTAY) 8 9 # What I need is based on this information, I need to find the actual value of Ax. 1.0403973607616896 8231.771911056438 In [ ]: 1 assert isinstance (Dx0, float), "Check that DxO is the norm of a vector." 2 print("Checkpoint 1.6 passed") Exercise 1(e) Repeat Exercise 1(d) with matrix B. If B(y + Ay) = b + Ab, where By = b and B, b, Ab are all defined above, determine Ay. Record your answer as the variable DYO where DYO has the value ||4y|l, where the norm is the 2-norm. Are the norms you computed in 1(d) and 1(e) smaller/larger than you expected, given the approximations of 1(b) and 1(c)? In [ ]: 1 # YOUR CODE HERE In [ ]: i assert isinstance (DYO, float), "Check that DYO is the norm of a vector." 2 print("Checkpoint 1.8 passed")