Exercise $2\mathrm{.}56.(*********)$

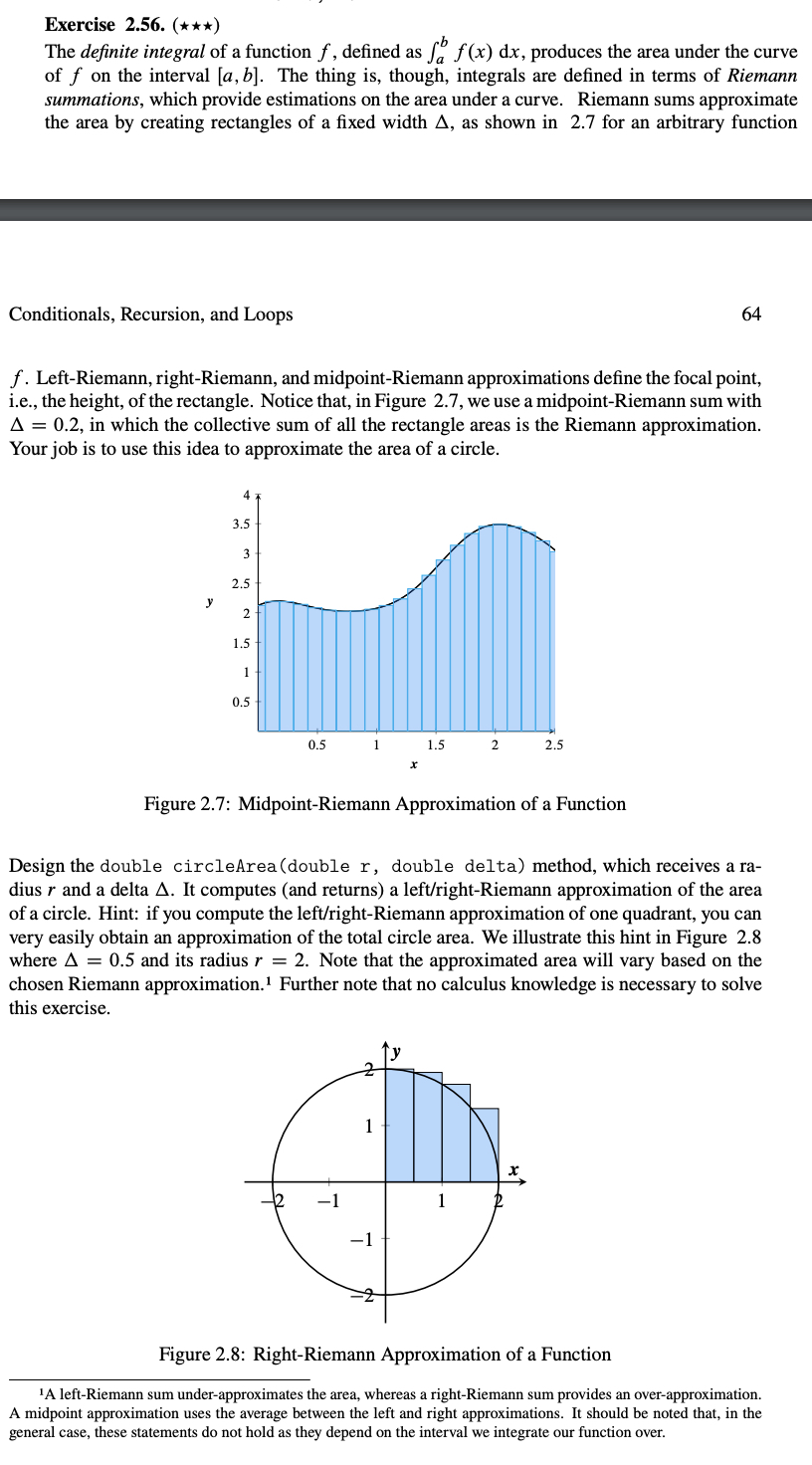
The definite integral of a function $f,$ defined as ${\displaystyle \underset{a}{\overset{b}{}}}f(x)dx,$ produces the area under the curve of $f$ on the interval $a,b.$ The thing is$,$ though, integrals are defined in terms of Riemann summations, which provide estimations on the area under a curve. Riemann sums approximate the area by creating rectangles of a fixed width $,$ as shown in $2\mathrm{.}7$ for an arbitrary function

Conditionals, Recursion, and Loops

$64$

$f.$ Left$-$Riemann, right$-$Riemann, and midpoint$-$Riemann approximations define the focal point, i$.$e$.,$ the height, of the rectangle. Notice that, in Figure $2\mathrm{.}7,$ we use a midpoint$-$Riemann sum with $=0\mathrm{.}2,$ in which the collective sum of all the rectangle areas is the Riemann approximation. Your job is to use this idea to approximate the area of a circle.

Figure $2\mathrm{.}7$: Midpoint$-$Riemann Approximation of a Function

Design the double circleArea$($double $r,$ double delta$)$ method, which receives a radius $r$ and a delta $.$ It computes $($and returns$)$ a left$/$right$-$Riemann approximation of the area of a circle. Hint: if you compute the left$/$right$-$Riemann approximation of one quadrant, you can very easily obtain an approximation of the total circle area. We illustrate this hint in Figure $2\mathrm{.}8$ where $=0\mathrm{.}5$ and its radius $r=2.$ Note that the approximated area will vary based on the chosen Riemann approximation. ${?}^1$ Further note that no calculus knowledge is necessary to solve this exercise.

Figure $2\mathrm{.}8$: Right$-$Riemann Approximation of a Function

${?}^1$A left$-$Riemann sum under$-$approximates the area, whereas a right$-$Riemann sum provides an over$-$approximation. A midpoint approximation uses the average between the left and right approximations. It should be noted that, in the general case, these statements do not hold as they depend on the interval we integrate our function over.