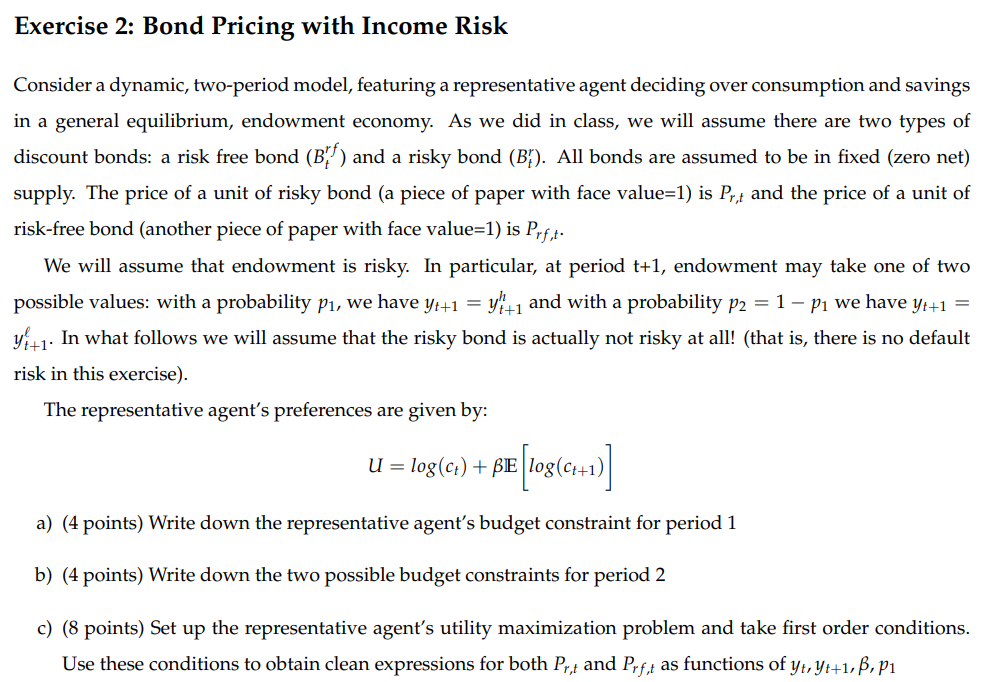
Exercise 2: Bond Pricing with Income Risk Consider a dynamic, two-period model, featuring a representative agent deciding over consumption and savings in a general equilibrium, endowment economy. As we did in class, we will assume there are two types of discount bonds: a risk free bond (B;-'r ) and a risky bond (Bf). All bonds are assumed to be in fixed (zero net) supply. The price of a unit of risky bond (a piece of paper with face value=1) is P;; and the price of a unit of risk-free bond (another piece of paper with face value=1) is Py . We will assume that endowment is risky. In particular, at period t+1, endowment may take one of two possible values: with a probability p1, we have y;11 = yi' 41 and with a probability p = 1 p; we have y;1 = y +1- In what follows we will assume that the risky bond is actually not risky at all! (that is, there is no default risk in this exercise). The representative agent's preferences are given by: U = log(ct) + BE {Iog(q)} a) (4 points) Write down the representative agent's budget constraint for period 1 b) (4 points) Write down the two possible budget constraints for period 2 c) (8 points) Set up the representative agent's utility maximization problem and take first order conditions. Use these conditions to obtain clean expressions for both P, ; and P, t as functions of vy, ye+1, B, 1 (once you have the first order conditions properly written, remember to impose the general equilibrium condition that y; = ; and ;1 = ;+1, since we assume bonds in zero net supply). In what follows, assume the following calibration: p = 0.9, y; = 2, y'{' 1 =23, yf =18 p1=05 d) (2 points) Compute the values for P, ;,P,,. Compute also the yields for each bond. e) (2 points) Based on the previous result you just obtained, comment on why there is no risk premium in this model