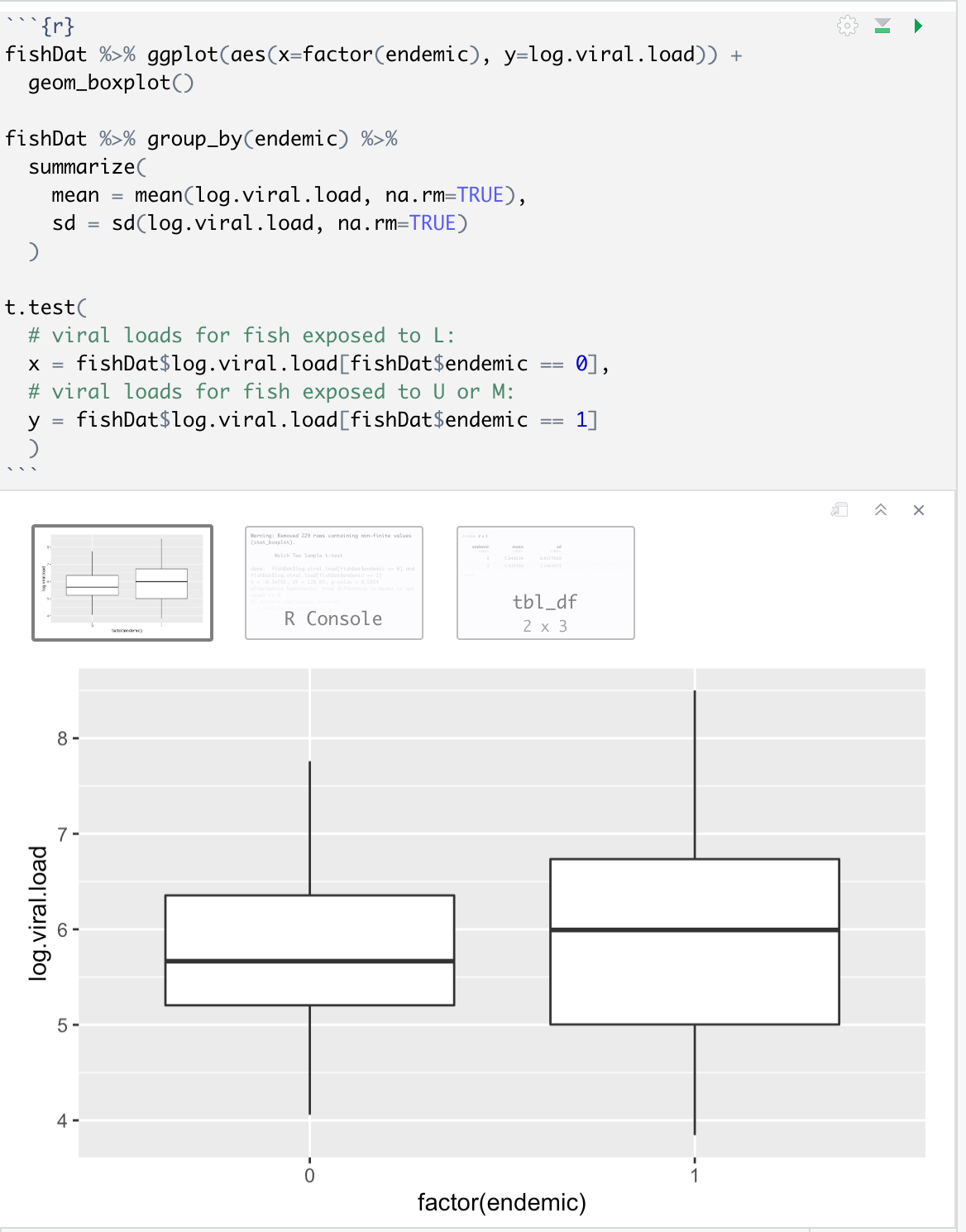
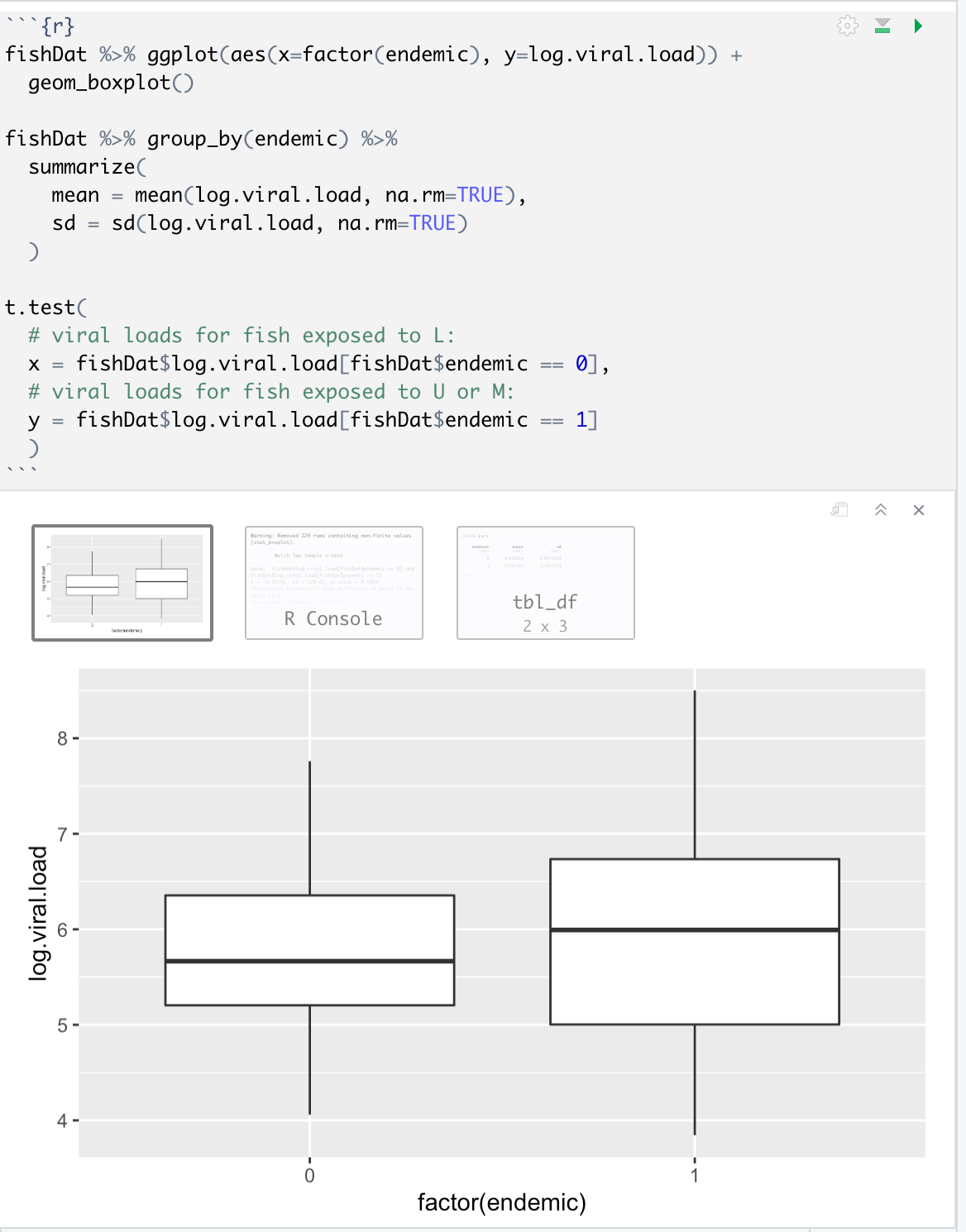
# Exercise 2 The following chunk performs another test of independence between the endemic/exotic strain variable (an indicator variable) and the log viral load variable. Viral strain may be thought of as the explanatory (independent) variable and log viral load as the response (dependent) variable. This test is based on the T distribution, which tests the hypothesis $$H_@:\\mu_{endemic}=\\mu_{exotic}$$ >> H0 2 \"endemic = \"exotic and therefore $$H_@:\\Delta\\mu\\triangleq\\mu_{endemic}\\mu_{exotic}=0$$ >> H0 2 AH \"endemic _ \"exotic = 0 {r} fishDat %% ggplot(aes(x=factor(endemic), y=log. viral. load)) + geom_boxplot() fishDat %>%% group_by(endemic) %% summarize( mean = mean(log. viral . load, na. rm=TRUE), sd = sd(log. viral . load, na. rm=TRUE) t. test( # viral loads for fish exposed to L: x = fishDat$log. viral. load[fishDat$endemic == 0], # viral loads for fish exposed to U or M: y = fishDat$log. viral . load[fishDat$endemic == 1] X Warning: Removed 229 rows containing non-finite values tbl_df R Console 2 x 3 8 - 7 - log.viral.load 6 - 5 - 4 . - - O - factor(endemic)The P-value For this test of independence is 0.2498. *Given what you know about tests of independence and what you know about Pvalues, what should you conclude about the null hypothesis (one sentence)? What does this lead you to conclude about the association between the endemic/exotic strain variable and the log viral load variable (one sentence)?* ***