Exercise 2.2.10 (Challenging): Let

{x_(n)}

be a convergent sequence such that

x_(n)>=0

and

kinN

. Then\

\\\\lim_(n->\\\\infty )x_(n)^((1)/(k))=(\\\\lim_(n->\\\\infty )x_(n))^((1)/(k)).

\ Hint: Find an expression

q

such that

(x_(n)^((1)/(k))-x^((1)/(k)))/(x_(n)-x)=(1)/(q)

.

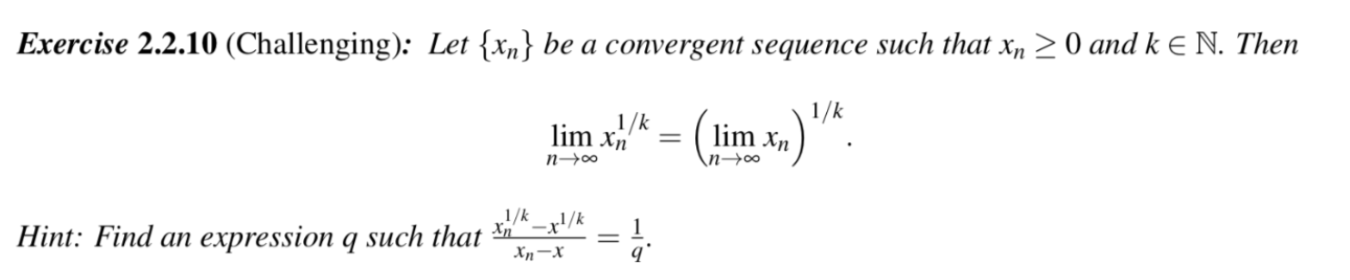
Exercise 2.2.10 (Challenging): Let {xn} be a convergent sequence such that xn0 and kN. Then limnxn1/k=(limnxn)1/k. Hint: Find an expression q such that xnxxn1/kx1/k=q1