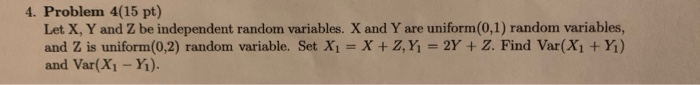
Exercise 24 (#1.58(c)). Let X and Y be random variables having the bivariate normal distribution with EX = EY = 0, Var(X ) = Var(Y) = 1, 18 Chapter 1. Probability Theory and Cov(X, Y) = p. Show that E(max { X, Y}) = V(1 -p)/*.4. Problem 4(15 pt) Let X, Y and Z be independent random variables. X and Y are uniform(0,1) random variables, and Z is uniform(0,2) random variable. Set X1 = X + Z, Y, = 2Y + Z. Find Var(X1 + Yi) and Var(X1 - Yi)