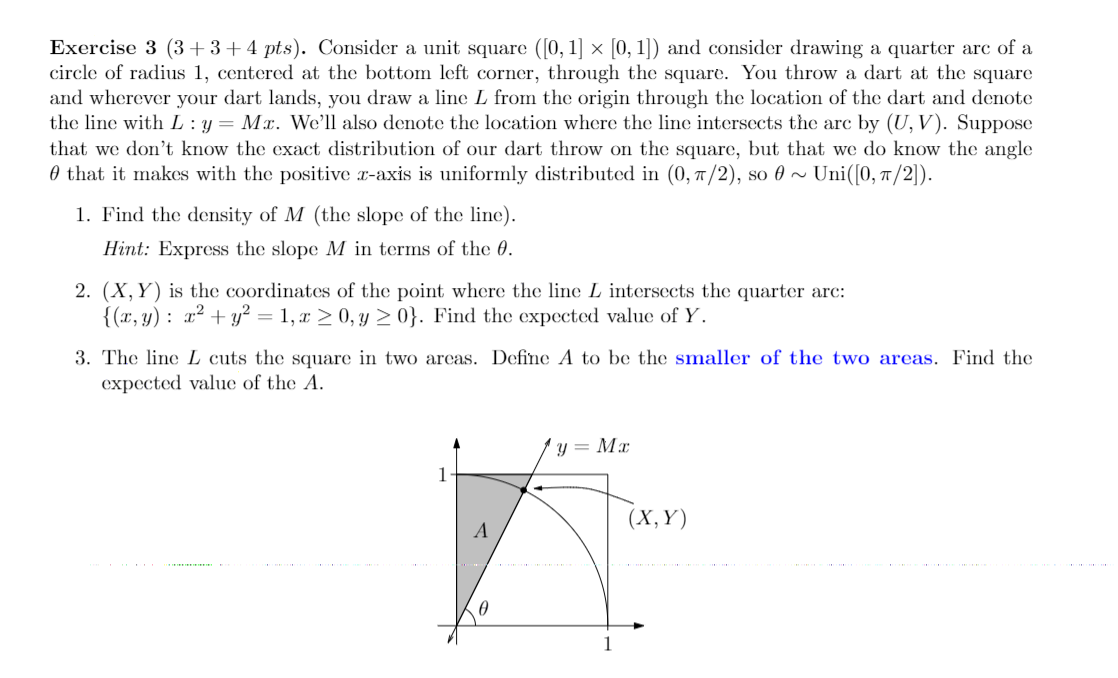
Exercise 3 (3 + 3 + 4 1758). Consider a unit square ([0,1] x [0,1]) and consider drawing a quarter are of a circle of radius 11 centered at the bottom left corner, through the square. You throw a dart at the square and wherever your dart lands, you draw a line L from the origin through the location of the dart and denote the line with L : y = M us. We'll also denote the location where the line intersects the are by (U , V). Suppose that we don't know the exact distribution of our dart throw on the square, but that we do know the angle 6 that it makes with the positive :raxis is uniformly distributed in (0,1T/2], so 6 N Uui([0,Tr/2]]. 1. Find the density of M (the slope of the line). Hint: Express the slope M in terms of the 9. 2. (X, Y) is the coordinates of the point where the line L intersects the quarter are: {(11510 : :32 + y2 = 1,3: 2 0,1; 2 0}. Find the expected value of Y. 3. The line L cuts the square in two areas. Dene A to be the smaller of the two areas. Find the expected value of the A. y=Mx (XaY)