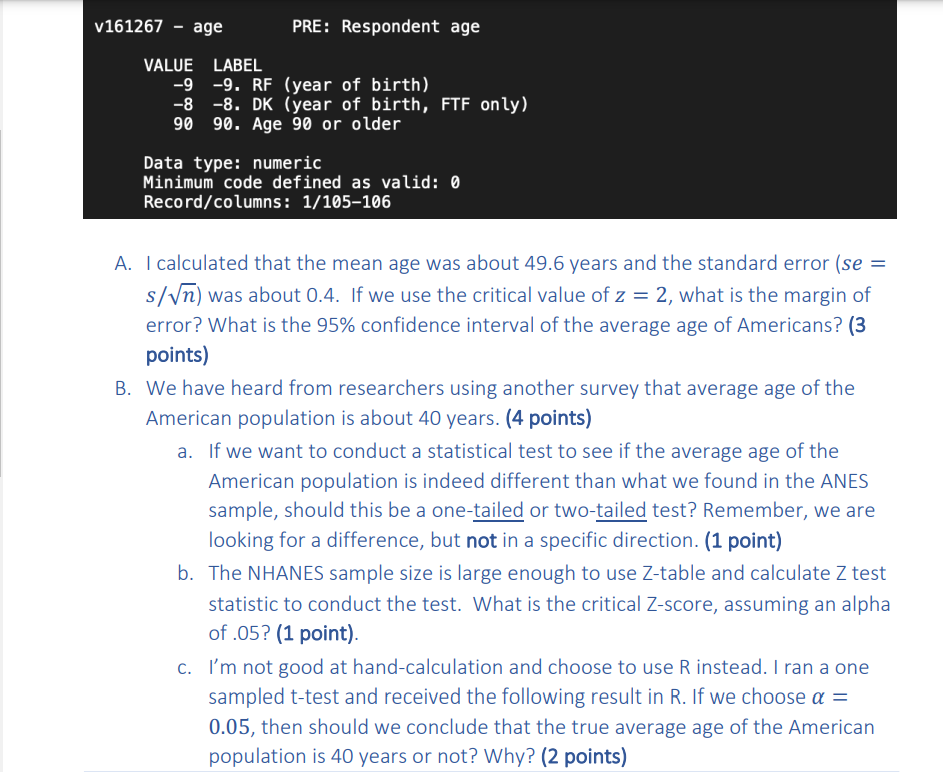
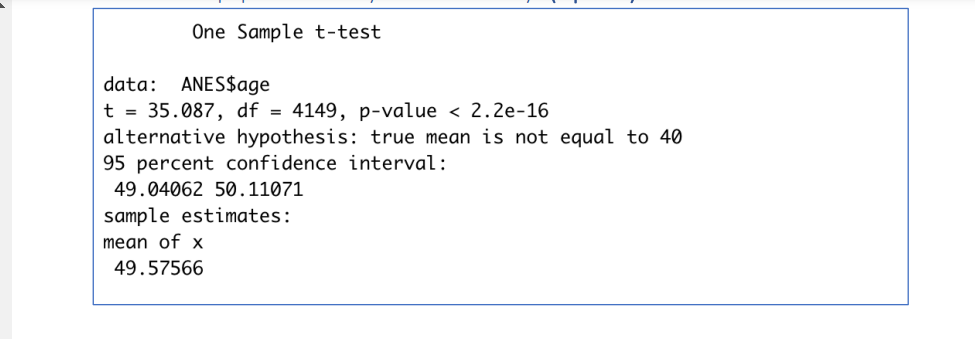
Exercise 4: Confidence Intervals, Comparing Means, and Comparing Percentages (17 points) The variable v161267 represents NHANES participants' age in years at the time of survey screening. Individuals aged 90 and over are top-coded at 90 years of age, as shown below. v161267r age PRE: Respondent age LABEL -9. RF {year of birth} 8. DK {year of birth, FTF only} 96. Age 98 or older Data type: numeric Minimum code defined as valid: 6 Reco rd/cotumns: 1/155166 A. I calculated that the mean age was about 49.6 vears and the standard error {58 = S/Jl was about 0.4. ll'we use the critical value of z = 2, what is the margin of error? What is the 95% confidence interval of the average age of Americans? (3 points) B. We have heard from researchers using another survev that average age of the American population is about 40 years. (4 points) a. If we want to conduct a statistical test to see if the average age of the American population is indeed different than what we found in the AN ES sample, should this be a onetailed or twotailed test? Remember, we are looking for a difference, but not in a specific direction. (1 point) b. The NHANES sample size is large enough to use Ztable and calculate Z test statistic to conduct the test. What is the critical Zscore, assuming an alpha of .05? (1 point). c. I'm not good at handcalculation and choose to use R instead. I ran a one sampled ttest and received the following result in R. If we choose a : 0.05, then should we conclude that the true average age of the American population is 40 years or not? Why? (2 points) One Sample ttest data: ANES$age t = 35.087, dF = 4149, pValue