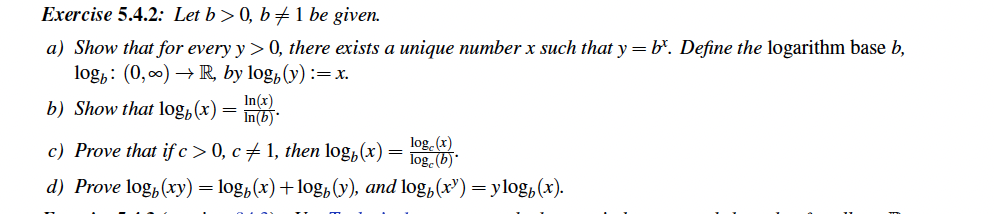
Exercise 5.4.2: Let b > 0, b / 1 be given. a) Show that for every y > 0, there exists a unique number x such that y = b*. Define the logarithm base b, logb: (0, co) - R, by logb (y) : =x. b) Show that logb (x) = In(6)' In(x) c) Prove that if c > 0, c # 1, then logb (x) = log. (6)' log (x) d) Prove log,(xy) = logb(x) + log, (y), and log (x)) = vlog (x)