Exercise $6$: Rigid body buckling

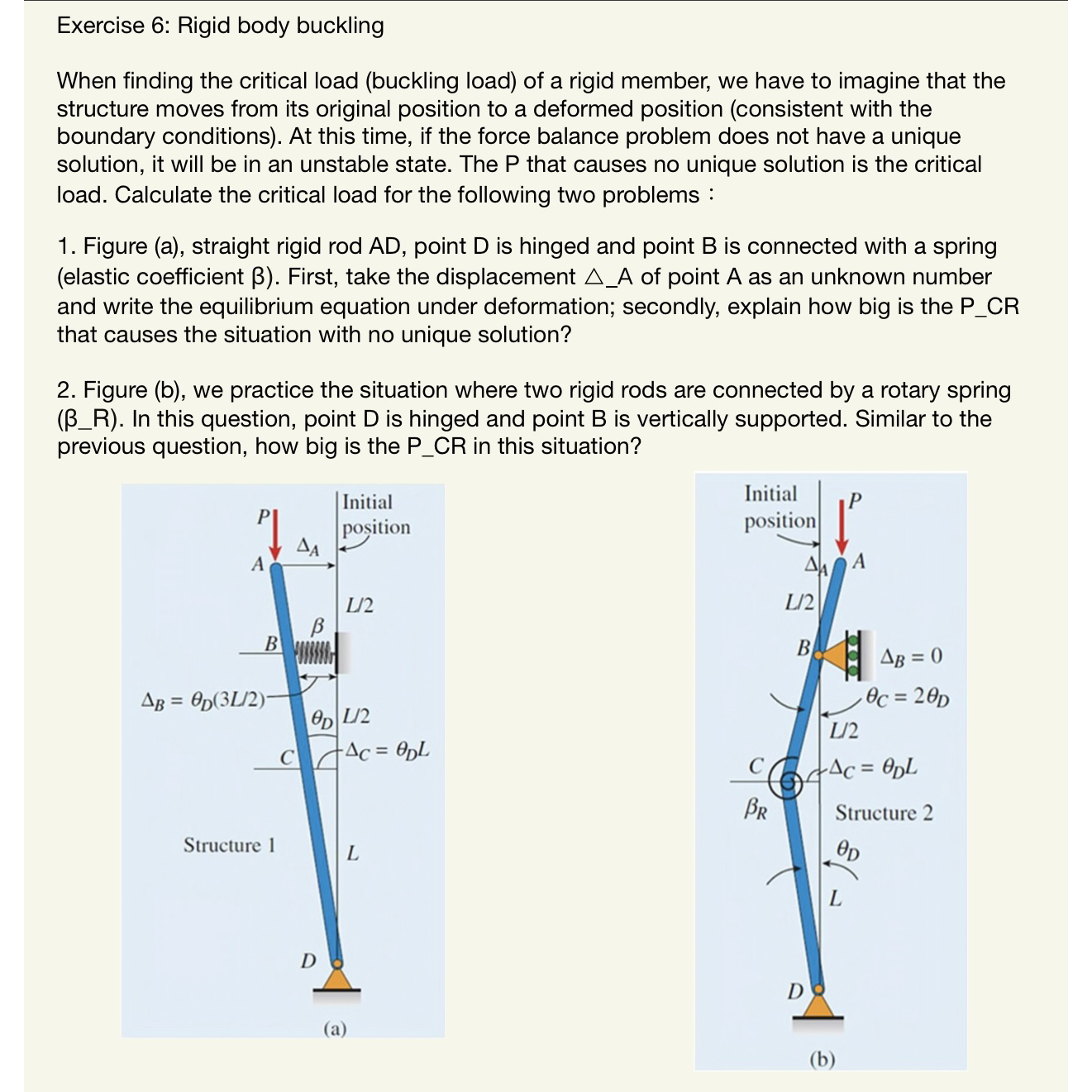
When finding the critical load $($buckling load$)$ of a rigid member, we have to imagine that the structure moves from its original position to a deformed position $($consistent with the boundary conditions$).$ At this time, if the force balance problem does not have a unique solution, it will be in an unstable state. The $P$ that causes no unique solution is the critical load. Calculate the critical load for the following two problems :

Figure $($a$),$ straight rigid rod $AD,$ point $D$ is hinged and point $B$ is connected with a spring $($elastic coefficient $).$ First, take the displacement $\frac{?}{{?}_{\frac{?}{?}}{?}_{-}A}$ of point $A$ as an unknown number and write the equilibrium equation under deformation; secondly$,$ explain how big is the P$\_$CR that causes the situation with no unique solution?

Figure $($b$),$ we practice the situation where two rigid rods are connected by a rotary spring $({}_R).$ In this question, point $D$ is hinged and point $B$ is vertically supported. Similar to the previous question, how big is the P$\_$CR in this situation?