Question: EXERCISES ( a ) Consider the modified problem ( d ^ ( 2 ) y ) / ( dt ^ ( 2 ) ) +
EXERCISES
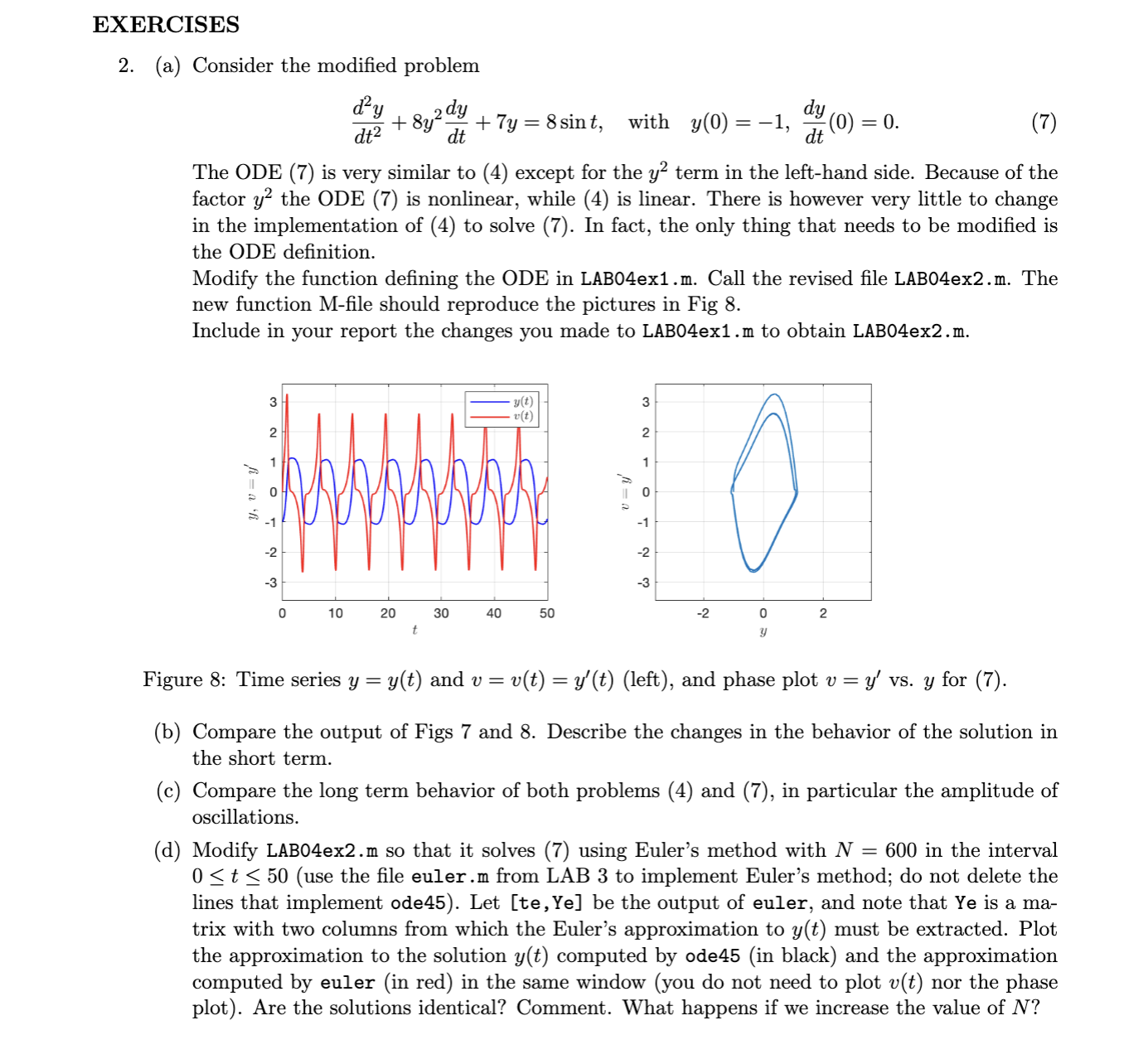
a Consider the modified problem
dydtydydtysint with ydydt
The ODE is very similar to except for the y term in the lefthand side. Because of the
factor y the ODE is nonlinear, while is linear. There is however very little to change
in the implementation of to solve In fact, the only thing that needs to be modified is
the ODE definition.
Modify the function defining the ODE in LABOexm Call the revised file LABOexm The
new function Mfile should reproduce the pictures in Fig
Include in your report the changes you made to LABOexm to obtain LABOexm
Figure : Time series yyt and vvtytleft and phase plot vy vs y for
b Compare the output of Figs and Describe the changes in the behavior of the solution in
the short term.
c Compare the long term behavior of both problems and in particular the amplitude of
oscillations.
d Modify LABexm so that it solves using Euler's method with N in the interval
tuse the file euler.m from LAB to implement Euler's method; do not delete the
lines that implement ode Let te Ye be the output of euler, and note that Ye is a ma
trix with two columns from which the Euler's approximation to yt must be extracted. Plot
the approximation to the solution ytvt nor the phase
plotN
exwitheqs.m
t; tf ; y;;
a ; b ; c ; d ;
ty ode@fttfyabcd;
u y:; u y:; y in output has columns corresponding to u and u
figure;
subplot; plottub; ylabelu;
subplot; plotturo; ylabelu;
figure
plotuu; axis square; xlabelu; ylabelu; plot the phase plot
function dydt ftyabcd
u y; u y;
dydt aubuu ; cuduu;
end
exwithparam
function exwithparam
t; tf ; y;
a ;
ty ode@fttfya;
dispy numstrtend numstryend
displength of y numstrlengthy
end
function dydt ftya
dydt ayexptexpt;
end
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


