Expected value for an alternative can be determined using the relationship: EMV = PayoffiProbability of Payoffi

Expected value for the Alternative 1 option = $_________

(response should be rounded to nearest whole number)

Expected value for the Alternative 2 option = $_________

(response should be rounded to nearest whole number)

Expected value for the Alternative 3 option = $_________

(response should be rounded to nearest whole number)

The alternative that provides Robert the greatest expected monetary value (EMV) is _______?

The value of the return under this decision is $________ (response should be rounded to nearest whole number)

For calculating the expected value of perfect information, firstly we need to determine the EVwPI. Which is, EVwPI =

When demand is expected to be low, the best possible payoff is $________

When demand is expected to be high, the best possible payoff is $_______

The expected value with perfect information (EVwPI) = _______?

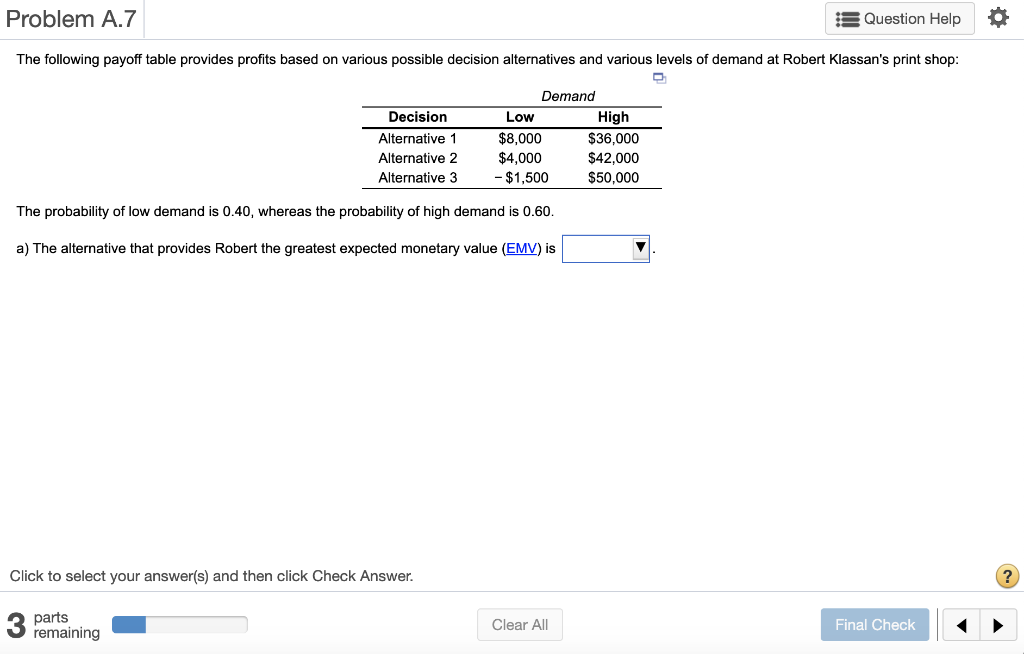
Problem A.7 s Question Help The following payoff table provides profits based on various possible decision alternatives and various levels of demand at Robert Klassan's print shop: Decision Alternative 1 Alternative 2 Alternative 3 Demand Low High $8,000 $36,000 $4,000 $42.000 - $1,500 $50,000 The probability of low demand is 0.40, whereas the probability of high demand is 0.60. a) The alternative that provides Robert the greatest expected monetary value (EMV) is Click to select your answer(s) and then click Check Answer. ? parts remaining Clear All Final Check