Explain all steps clearly and in detail.

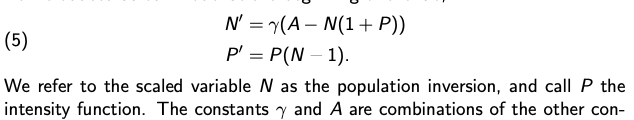
Exercise 4: A linear system that approximates (5) near (1, A - 1) is U' = -(Autv). v = (A-1)u. In this exercise we see how we can obtain this. (a) Let N = 1 + u and P = (A -1) + v. Plug these into the system (5) and expand. If u and v are both very small in magnitude, so that we can discard nonlinear terms, show that you obtain the linearized system above. (b) Plot (1, A-1) in the phase plane (by hand). What do u and v measure in the phase plane? The function Pro(t) = v(t) + A -1 is called the relaxation oscillation (RO) of the laser. How is it related to P? (c) Recall that in the objectives for this lab we noted that a linear system is equivalent to a single higher-order differential equation. Let's see that this is try here: notice that the second equation is equivalent to LAB 3: LASERS, LINEAR SYSTEMS, AND HARMONIC OSCILLATORS 5 u = A TV; use this in the first equation to obtain a single second-order linear equation for v.In! M\" = (A Nu; P (5) P' = P[N 1). We refer to the scaled 1I.raria|:I|e N as the population inversion, and call P the intensity function. The constants "y and A are combinations of the other con