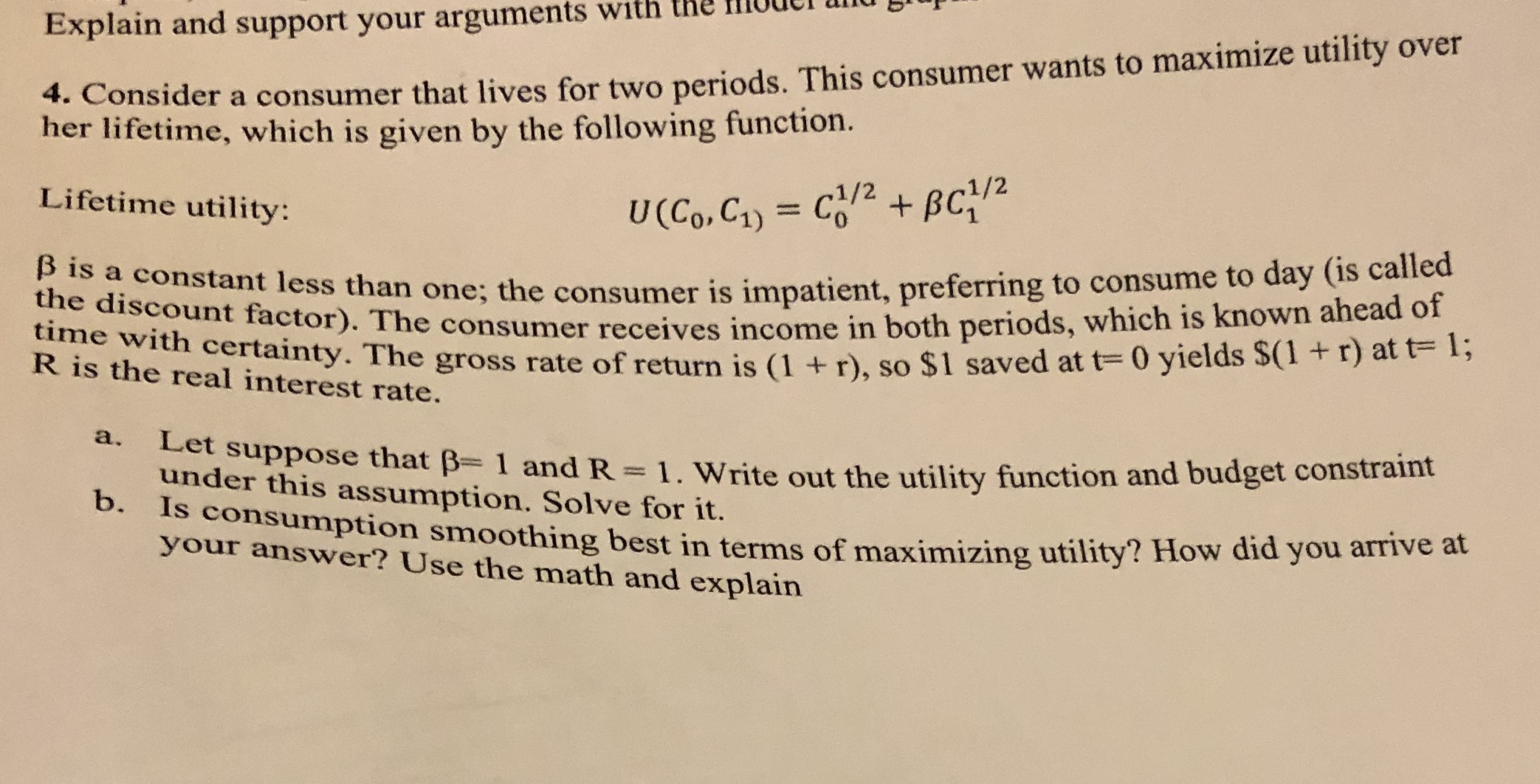
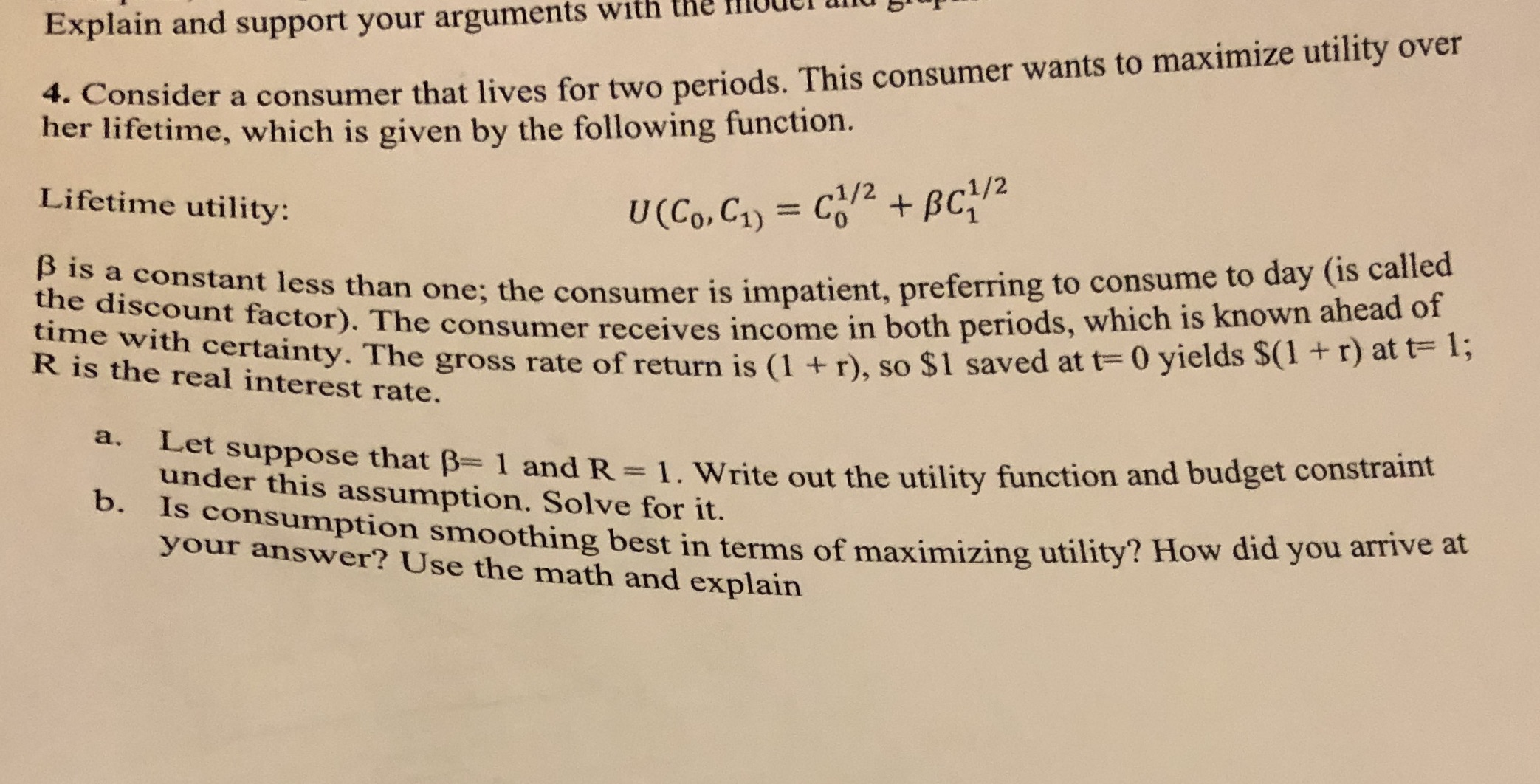
Explain and support your arguments with the mou 4. Consider a consumer that lives for two periods. This consumer wants to maximize utility over her lifetime, which is given by the following function. Lifetime utility: U(Co, C1) = C/2 + BC1/2 B is a constant less than one; the consumer is impatient, preferring to consume to day (is called the discount factor). The consumer receives income in both periods, which is known ahead of time with certainty. The gross rate of return is (1 + r), so $1 saved at t= 0 yields $(1 + r) at t= 1; R is the real interest rate. a. Let suppose that B= 1 and R = 1. Write out the utility function and budget constraint under this assumption. Solve for it. b. Is consumption smoothing best in terms of maximizing utility? How did you arrive at your answer? Use the math and explain