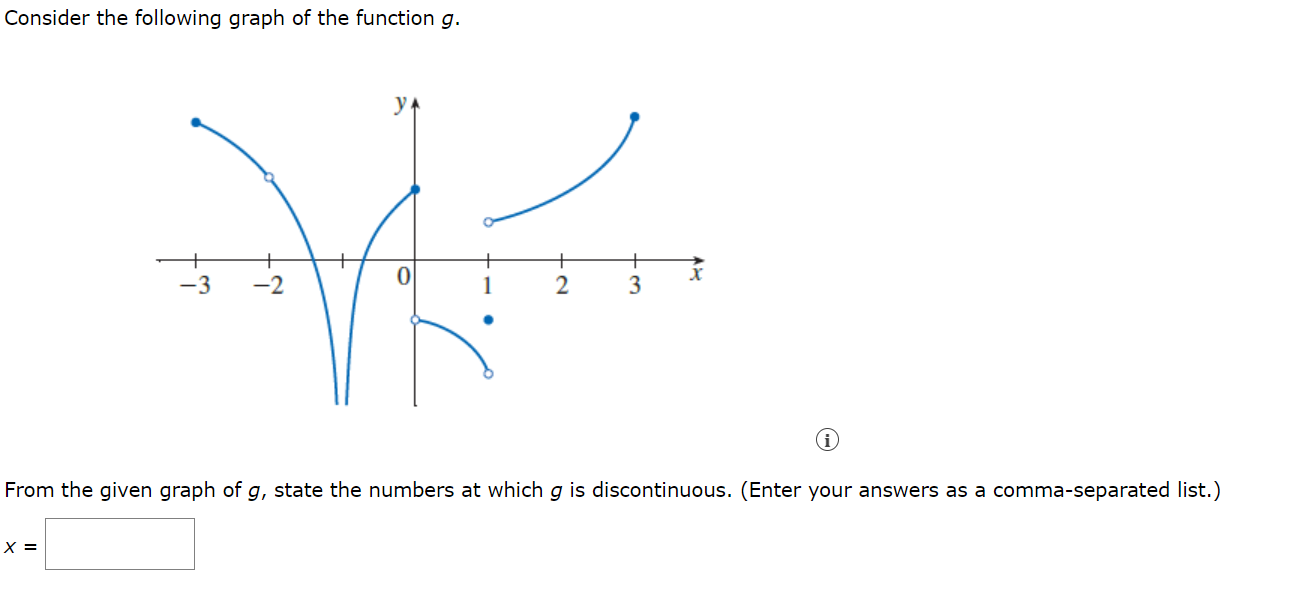
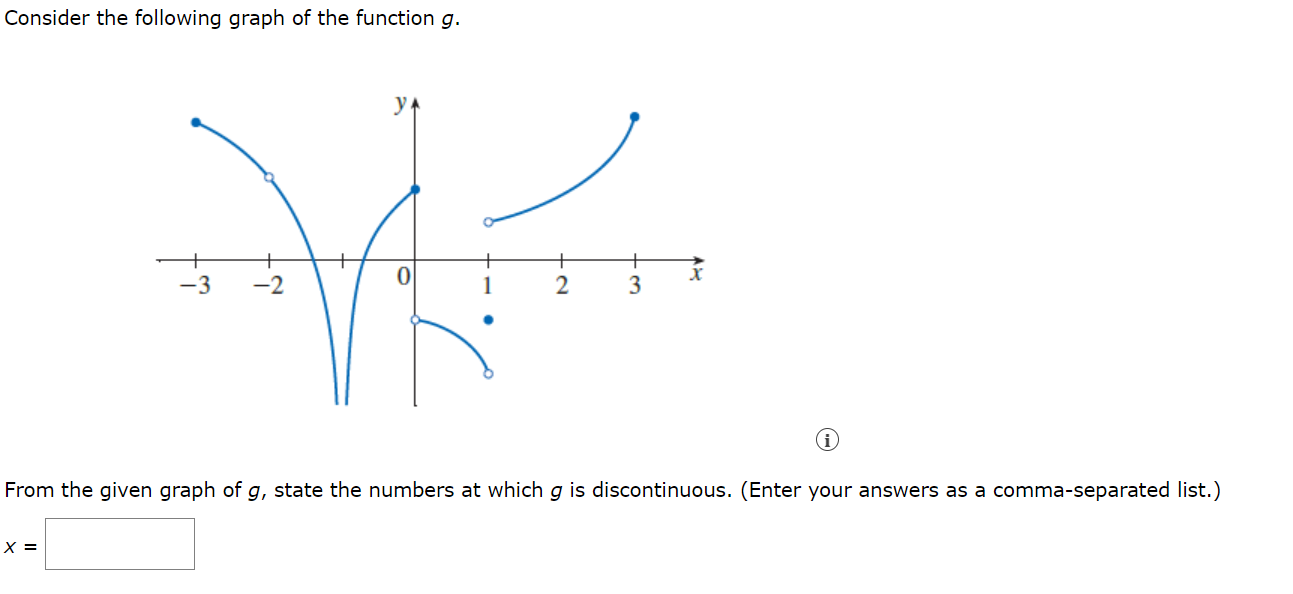
Explain why the function is discontinuous at the given number a. (Select all that apply.) x2 - 2x f ( x ) = if x * 2 x2 - 4 a = 2 if x = 2 O f(2) is undefined. lim f(x) does not exist. X- 2 O lim f(x) and lim f(x) are finite, but are not equal. x - 2+ X - 2- f(2) is defined and lim f(x) is finite, but they are not O X - 2 equal. O none of the aboveExplain why the function is discontinuous at the given number a. (Select all that apply.) f ( x ) = 1 a = -5 X + 5 Of(-5) and lim f(x) are finite, but are not equal. X- -5 lim f(x) and lim f(x) are not finite, and are not equal. X - -5+ X--57 lim f(x) does not exist. X- -5 O f(-5) is undefined. O none of the aboveUse the definition of continuity and the properties of limits to show that the function is continuous on the given interval. f ( x) = x+ Vx - 9, [9, 00) For a | ? v 9, we have lim f(x) = lim (x + vx-s x- a x - a = lim (x) + lim by the sum law x - a x - a = lim (x) + lim by the root law x - a x - a = lim (x) + lim lim (9) by the difference law x - a x - a x - a 9 by the direct substitution property Therefore, f is continuous at x = a for every a in (9, co). Also, lim f(x) = = f(9), so f is continuous from the right at 9. Thus, f is continuous on [9, co). x-9+Consider the following graph of the function g. G) From the given graph of g, state the numbers at which 9 is discontinuous. (Enter your answers as a comma-separated list.) X