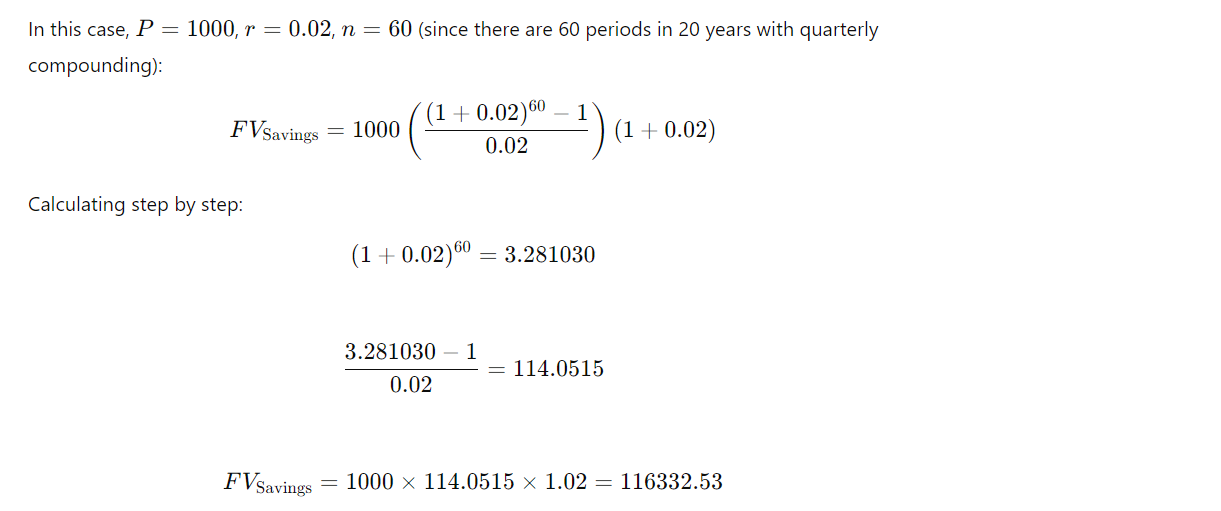
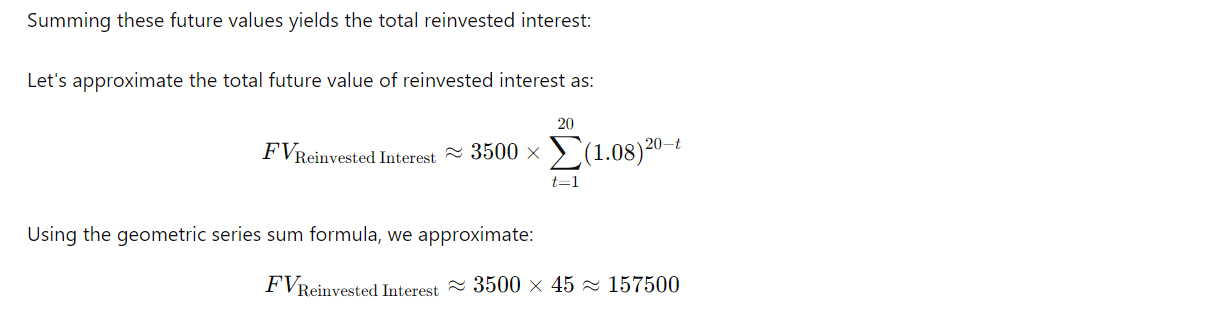
Extra credit assignment worth 5 points on exam 1 Jasmine deposits 1000 into a savings account paying nominal interest rate of 6 percent compounded three times a year. She decides to deposit the same amount at the beginning of each third of the year for 20 years. The interest earned from this account is withdrawn at the end of each year only and reinvested into another account earning AEIR 8%. Find the accumulated value of Jasmine's money in both accounts at the end of the 20 years. 1+ 6 = ( 1+ it ) = (1. 01) = 1. 0201 i (2) . 02 = .01 / 6 month i = . 0201 Annual . period The Justin Problem Justin deposits 100 into a savings account, paying nominal interest rate i(2) = 2 % at the beginning of each half year for 10 years. The interest earned from this account can be withdrawn at the end of each year and reinvested into another account earning AEIR 4%. Find the accumulated value of his holdings in both accounts at the end of 10 years. 100 100 100 100 100 Ay = 2,000 since all 100 100 interest is withdraw 2 10 annually. 2001 + 18001 + 100 5 21 - 01- 200 100521.01-200 100 521.01 200 1 =.04 10 At t= 1 , the deposit in the 4% acct is : 100 (1. 01) + 100 (1.01) 100 - 100 100 (1. 01) + 100 (1.01) - 200 At t = 2 , there will be interest on the 100 $ 21. 01 - 200 Generated Interest on yr ! $ 200 present at t= 1 of 200 1 deposits plus the interest on the yr. 2 deposits of (100 527.01 - 200 interest on fresh At t= 3 , there will be interest on the 400 present of 40ol + 100 521..7. dep . - 200 At t= 10 , interest = 18001 + 100 5,]. - 200 AU Total = 2, 000 + ( Ip, Q s ) iol.OH P = 100 51.0 - 200 = 3.01 time 10 Q = 2001 = 200 (.0201 ) = 4.02 = 2,000 + PSni + Q (Spi - n) Siol. OF ( 1.04 ) - 1 . 04 = 2,000 + (3.01) (12. 00610712) + 4.02 (12.00610 712 - 10) = 12. D0610712 . 04 2, 000 + 36 . 138 + 201. 614 = 2, 237. 75 what would be the error if you withdrew the interest every 6 mos ? Interest acct 2000 + ( Ip , a 5) 201 . 01980 3903 100(.01) 200(-01) 3 20 Pal , Q = 1 24 . ". It " = ( It is ) ? 10 2000 + 1( + 480944285)+ 1 (+48.... -2 24-24998204 1.04 = 1+64 5201 019803 903 = 480444985 . 019803903 "A= '9 98039 03 2 , 238. 85 = 24. 249 98209 | Error = 2, 238.85 - 2, 237. 75 = 1.10Part 1: Savings Account with Quarterly Compounding 1. Identify the variables for the savings account: . Initial deposit each period (P) = $1000 . Nominal annual interest rate (r) = 6% . Compounding periods per year (n) = 3 . Total number of years (t) = 20 2. Calculate the periodic interest rate: 0.06 Periodic interest rate = 0.02 n 3 3. Future Value of the Deposits To calculate the future value of the savings account with deposits made at the beginning of each period, we use the formula for the future value of an annuity due: FV Annuity Due = P (1+r)2 - 1 ( 1 + r ) rIn this case, P = 1000, r = 0.02, n = 60 (since there are 60 periods in 20 years with quarterly compounding): FVSavings = 1000 (1 + 0.02)60 - 1 (1 + 0.02) 0.02 Calculating step by step: (1 + 0.02) 60 = 3.281030 3.281030 - 1 = 114.0515 0.02 FVSavings = 1000 x 114.0515 x 1.02 = 116332.53Part 2: Reinvested Interest in the AEIR 8% Account 1. Calculate the yearly interest earned from the savings account The annual interest from the savings account is compounded quarterly: Annual Interest = Total Balance at the End of Year Total Balance at the Start of Since the interest is reinvested annually, we can assume the balance at the end of each year grows separately in an account with 8% AEIR. 2. Future Value of Reinvested Interest Each year's interest is compounded at 8% for the remaining years: 20 F'Vinterest = Z Interest,(1.08)% =1 3. Approximate Calculation for Reinvested Interest We'll calculate the interest for each year and compound it. This can be done precisely with a financial calculator, but let's outline the process: Assume the interest earned each year is reinvested. Each year's interest is approximately: 116332.53 Annual Interest = X 0.06 ~ 3490 20 Now, each annual interest is compounded for the remaining years at 8%: For year 1: 3490 x (1.08) ~3490 x 4.66 = 16255.4 For year 2: 3490 x (1.08)18 ~ 3490 x 4.31 = 15041.9Summing these future values yields the total reinvested interest: Let's approximate the total future value of reinvested interest as: 20 FVReinvested Interest ~ 3500 x (1.08) 20- t = 1 Using the geometric series sum formula, we approximate: FVReinvested Interest ~ 3500 x 45 ~ 157500Conclusion The accumulated value of Jasmine's money in both accounts at the end of 20 years is approximately