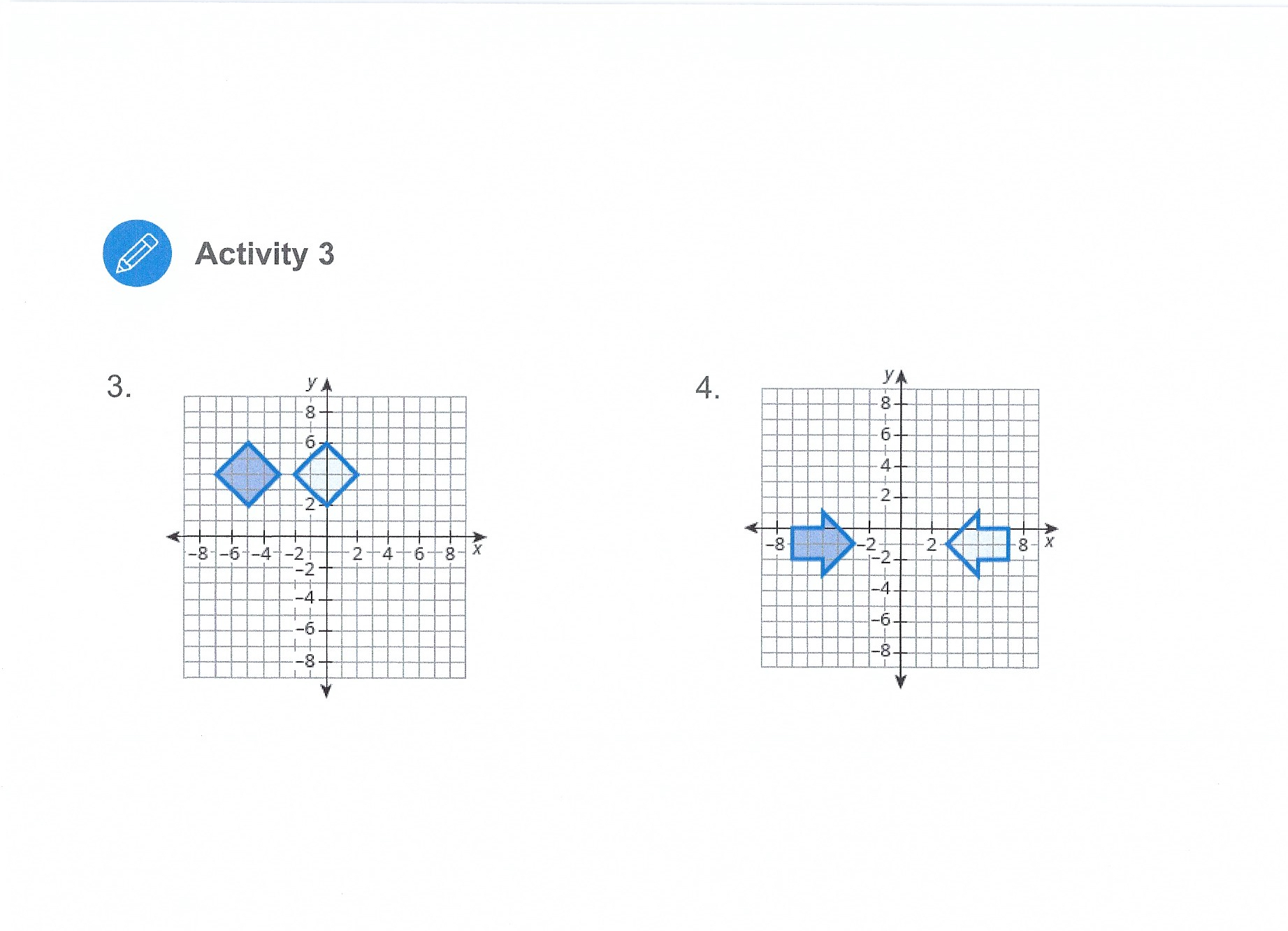
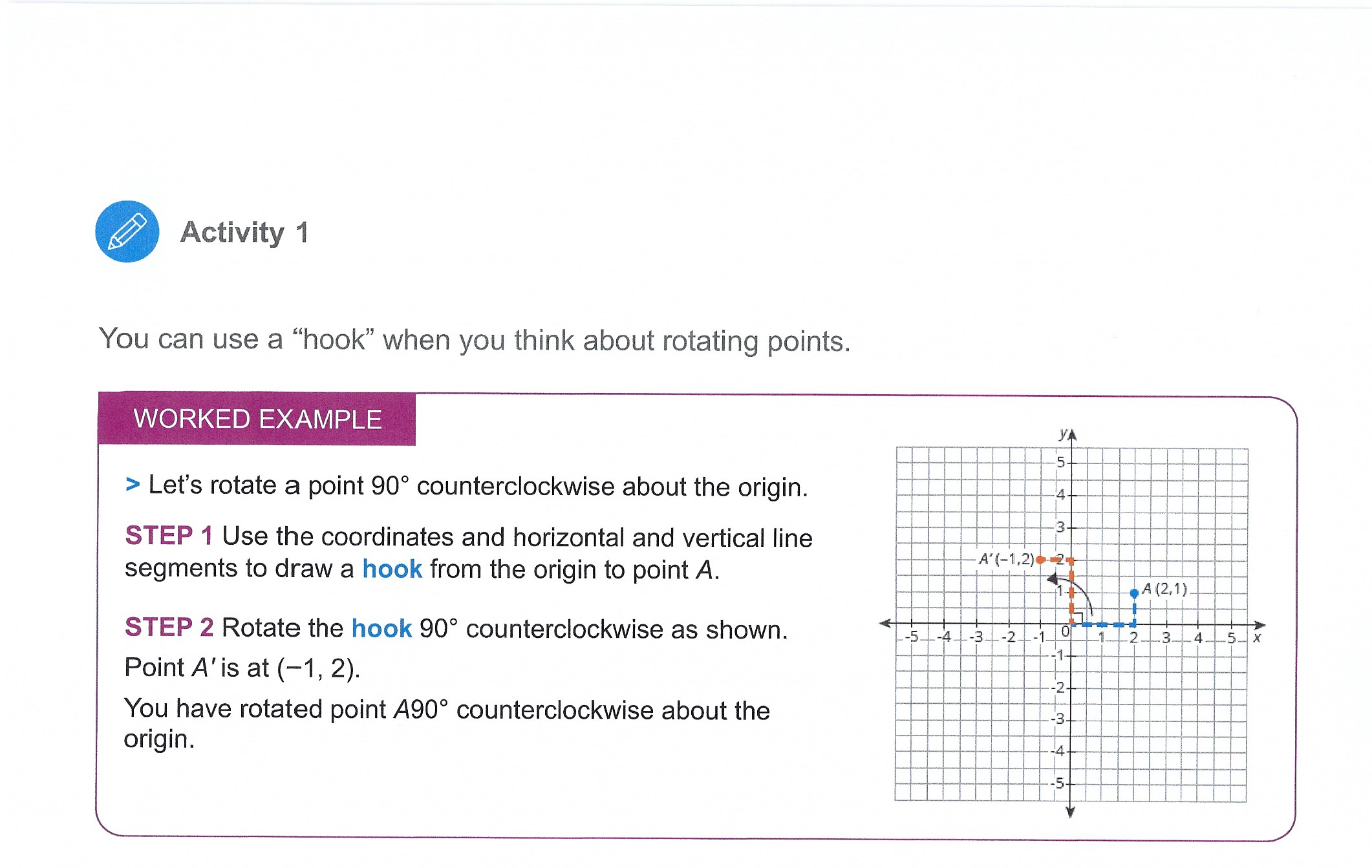
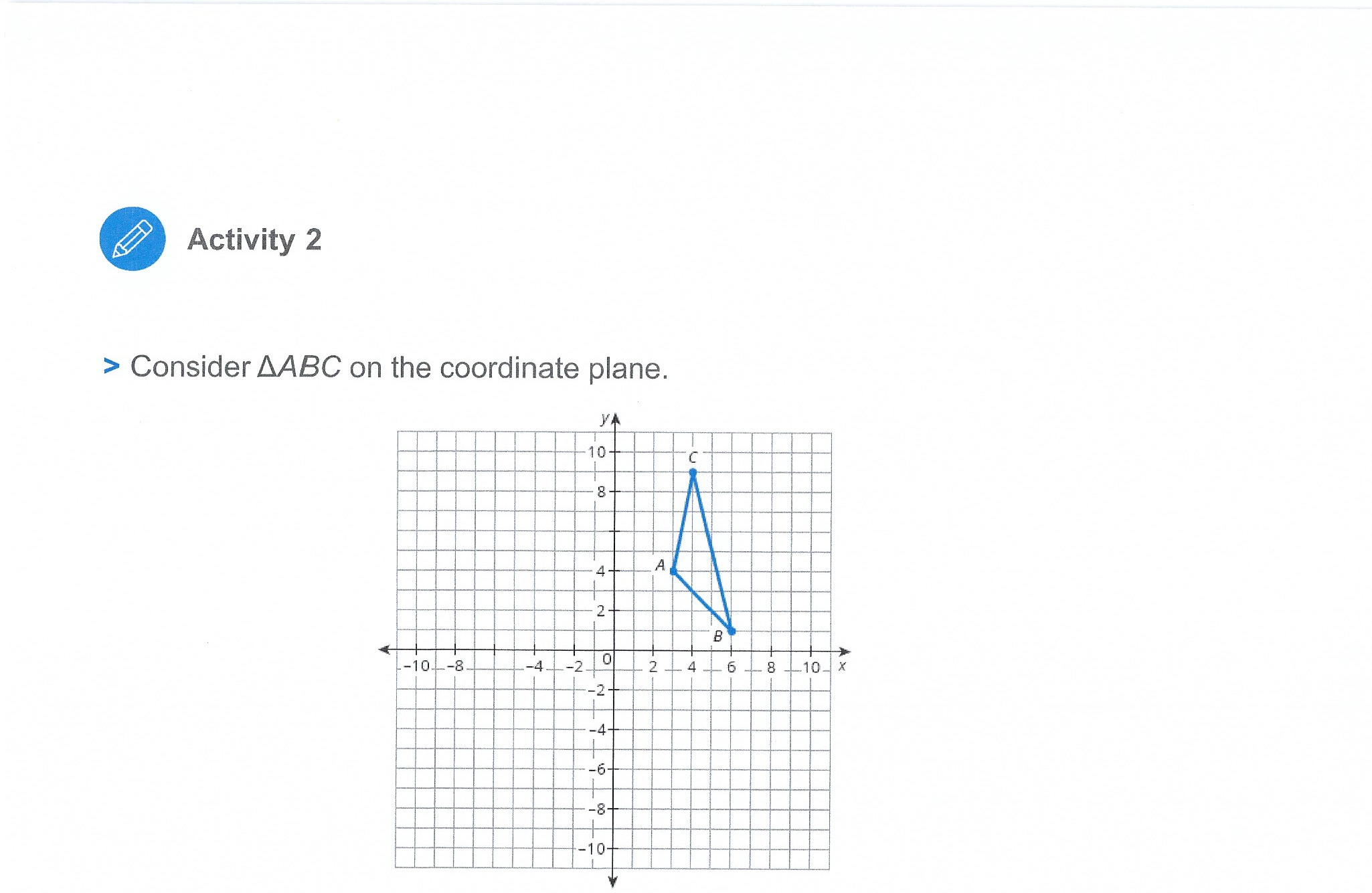
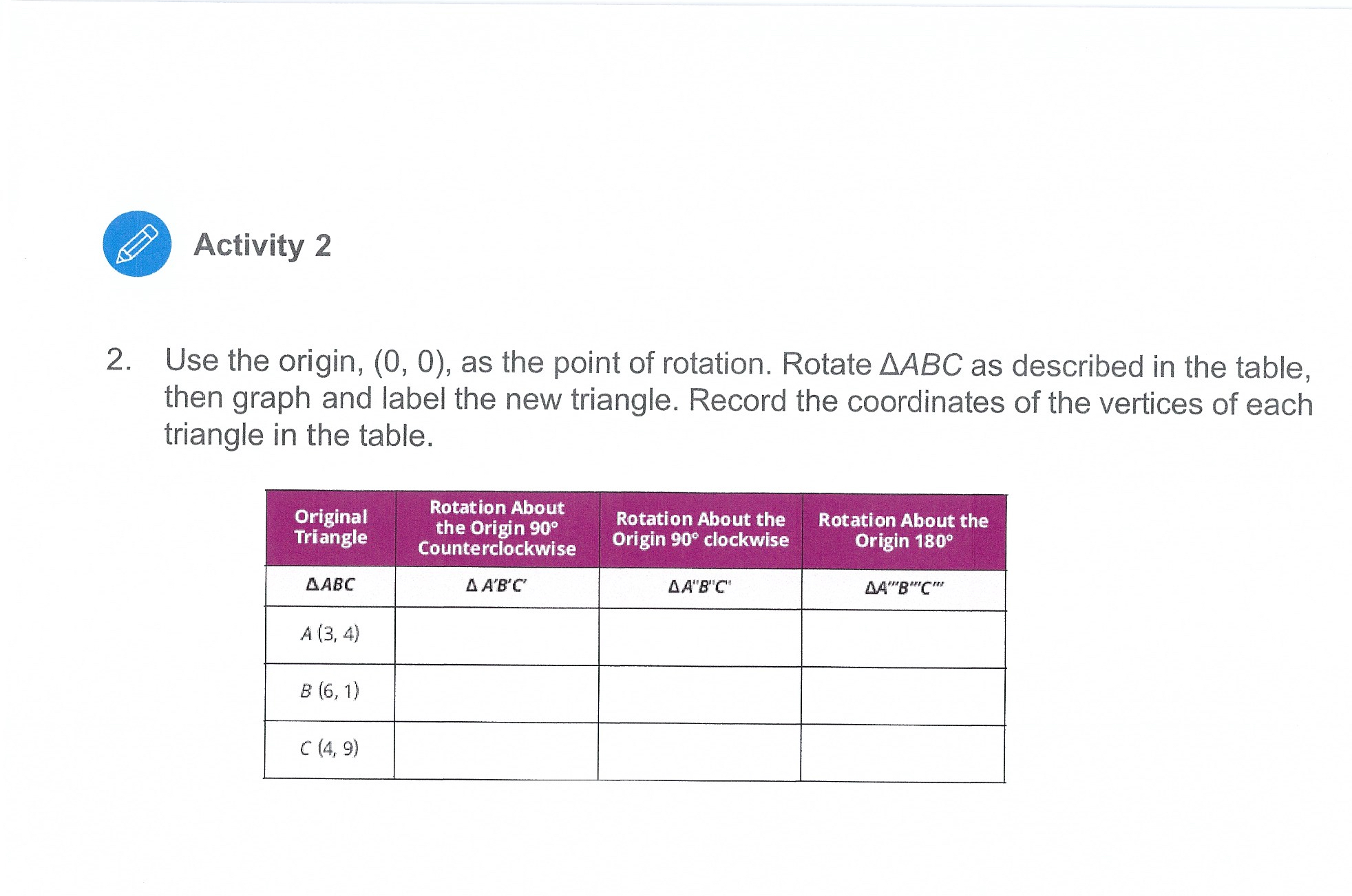
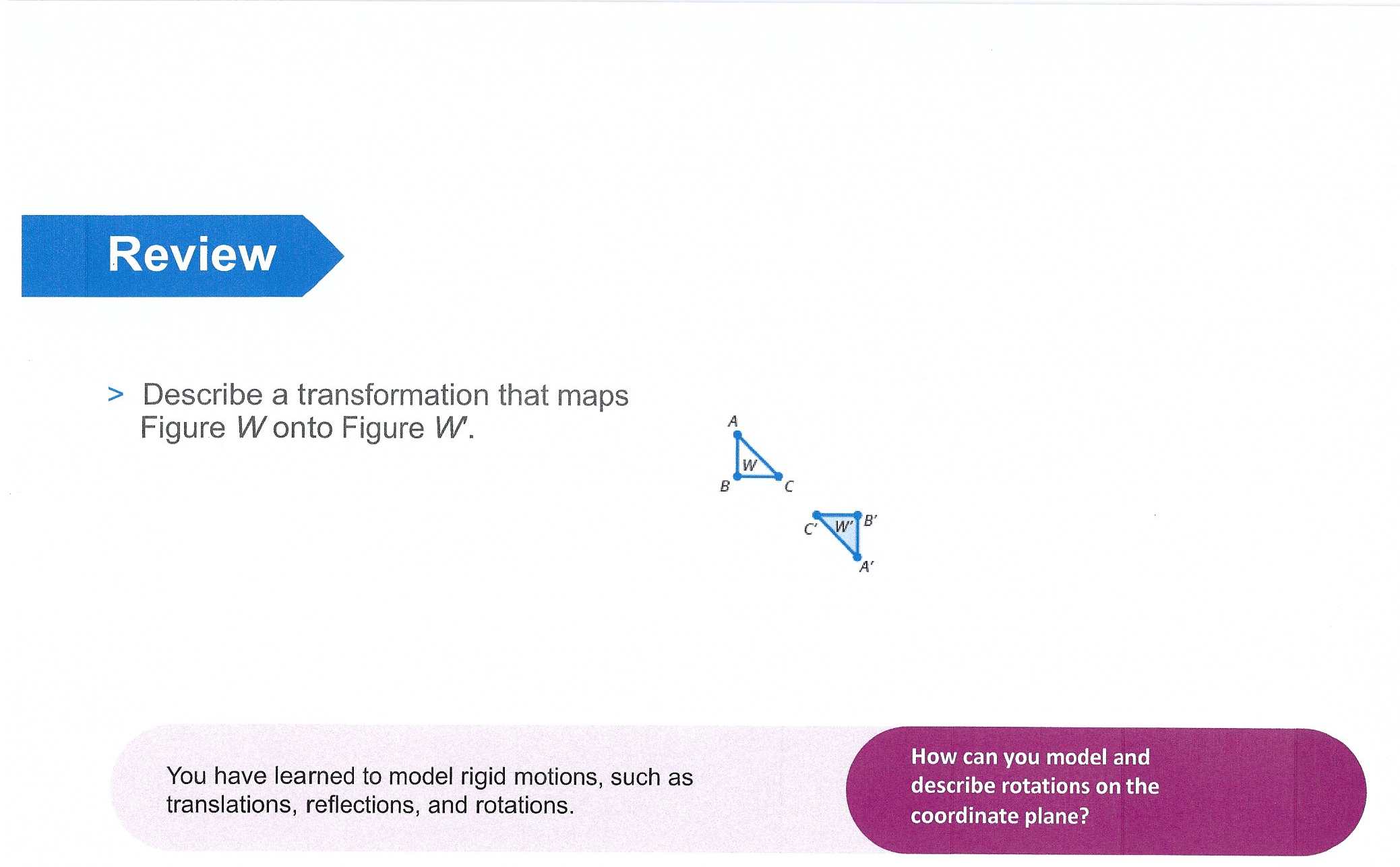
f ACthity 1 THINKING AND REASONING * Use patterns and structure to help understand and connect mathernatical concepis, Modeling Rotations on the Coordinate Plane In this activity, you will investigate rotating pre-images to understand how the rotation affects the coordinates of the image. 1. Rotate the figure 180 about the origin. a) Draw the figure, and the labels the coordinate points b) Mark the origin, (0, 0), as the center of rotation. Trace a ray from the origin along the x-axis. This ray will track the angle of rotation. Activity 3 THINKING AND REASONING . Demonstrate understanding by representing problems in multiple ways. Verifying Congruence Using Rigid Motions > Describe a rigid motion you could use to verify that the pre-image is congruent to the shaded image. 1. YA 2. 14- -8 -6 -4 -20 2 4 6 8 X -8 - 6 - 4- 24 8 x co- ateINActivity 3 3. YA 4. Natatook -8- -6- -4 -4- 6 -8 X -8 out of itTalk the Talk Just the Coordinates You can use what you know about rigid motions to verify that the figures represented by coordinates are congruent. > Verify that each pair of figures are congruent by describing the rigid motion. 1. Triangle QRS has coordinates Q (1, -1), R (3, -2), and S (2, -3). Triangle QU'R'S' has coordinates Q' (1, 1), R' (2, 3), and S' (3, 2). 2. Rectangle MNPQ has coordinates M (3, -2), N (5, -2), P (5, -6), and Q (3, -6). Rectangle M'N'P'Q' has coordinates M' (-3, 2), N' (-5, 2), P' (-5, 6), and Q' (-3, 6).Activity 1 c) Rotate the figure 180 about the center of rotation. Then, identify the coordinates of the rotated figure and draw the rotated figure on the coordinate plane. Finally, complete the table with the coordinates of the rotated figure. Coordinates of Pre-image Coordinates of Image Al2,1) d) Compare the coordinates of the rotated figure with the coordinates of the original figure. How are the values of the coordinates the same? How are they different? Explain your reasoning. Activity 1 You can use a \"hook\" when you think about rotating points. WORKED EXAMPLE > Let's rotate a point 90 counterclockwise about the origin. STEP 1 Use the coordinates and horizontal and vertical line segments to draw a hook from the origin to point A. STEP 2 Rotate the hook 90 counterclockwise as shown. Point A'is at (1, 2). You have rotated point A90 counterclockwise about the origin. Activity 1 2. How do you know you rotated the point 90? 3. What do you notice about the coordinates of the rotated point? > Now, let's investigate rotating a figure 90 about the origin. 4. Consider the parallelogram shown on the coordinate plane. a) Use the \""hook\" method to rotate the figure 90 counterclockwise about the origin. Then, identify the coordinates of the rotated figure and draw the rotated figure on the coordinate plane. Finally, complete the table with the coordinates of the rotated figure. Activity 1 Coordinates of Pre-image Coordinates of Image b) Compare the coordinates of the image with the coordinates of the pre-image. How are the values of the coordinates the same? How are they different? Explain your reasoning. 5. Make conjectures about how a counterclockwise 90 rotation and a 180 rotation affect the coordinates of any point (x, y). THINKING AND REASONING Activity 2 . Complete tasks with mathematical fluency. Rotating Any Points on the Coordinate Plane (x, y) > Consider the point (x, y) located anywhere in the first quadrant. 1. Use the origin, (0, 0), as the point of rotation. Rotate the point (x, y) as described in the table and plot and label the new point. Then record the coordinates of each rotated point in terms of x and y. THINK ABOUT.... How can you use Original Rotation About the Origin 90 Rotation About the Rotation About the an example like the Point Counterclockwise Origin 90 clockwise Origin 180 point (5, 1) to check your coordinates in (X, y) terms of x and y?Activity 2 > Consider AABC on the coordinate plane. C A , -10 -8. -4- 2 - 4-6 8 10-XActivity 2 2. Use the origin, (0, 0), as the point of rotation. Rotate AABC as described in the table, then graph and label the new triangle. Record the coordinates of the vertices of each triangle in the table. Rotation About T the Origin 90 Rotation About the = Rotation About the Origin 90 clockwise Lo dT-{0 R E-11 o g i) UL Counterclockwise Activity 2 > Let's consider rotations of a different triangle without graphing. 3. The vertices of ADEF are D(-7, 10), E(-5, 5), and F(-1, -8). a) b) c) If you rotate ADEF 90 counterclockwise about the origin, what are the coordinates of the vertices of the image? Name the rotated triangle. How did you determine the coordinates of the image without graphing the triangle? If you rotate ADEF 90 clockwise about the origin, what are the coordinates of the vertices of the image? Name the rotated triangle. How did you determine the coordinates of the image without graphing the triangle? If you rotate ADEF 180 about the origin, what are the coordinates of the vertices of the image? Name the rotated triangle. How did you determine the coordinates of the image without graphing the triangle? Review > Describe a transformation that maps Figure W onto Figure W. 4 B How can you model and You have learned to model rigid motions, such as describe rotations on the translations, reflections, and rotations. coordinate plane