Question: F: VV F(G(x)) = G(F(x)) Let V be an finite-dimensional linear space, and and linear in the transformation that is diagonalizable, that is: There

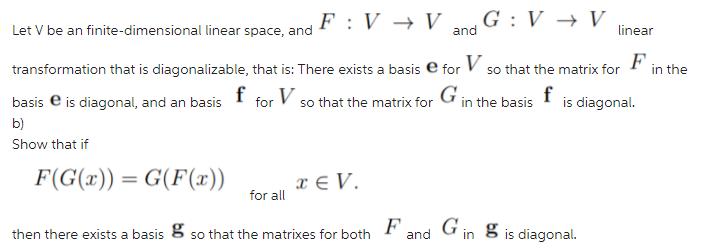
F: VV F(G(x)) = G(F(x)) Let V be an finite-dimensional linear space,

F: VV F(G(x)) = G(F(x)) Let V be an finite-dimensional linear space, and and linear in the transformation that is diagonalizable, that is: There exists a basis e for V so that the matrix for F basis e is diagonal, and an basis f for V so that the matrix for G in the basis f is diagonal. b) Show that if G: V V xEV. for all then there exists a basis so that the matrixes for both Fa and Gin g is diagonal.

Step by Step Solution

★★★★★

3.48 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Let V be an finitedimensional linear space and F VV and G VV be two linear transformations that are diagonalizable This means that there exist bases e and f for V such that the matrixes for F and G ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Let B = S-1 AS and let x be an eigenvector of B belonging to an eigenvalue show that S is an eigenvector of A belonging to .

For any quadratic form Q(x). xTAx, there exists a basis x1; x2; . . . , xn and numbers such that Q(x).

Let V be an n-dimensional vector space with basis B = {v1 , . . . , vn}. Let P be an invertible n X n matrix and set ui = p1iv1 + + pni vN for i = 1 , . . . , n. Prove that C = {u1 , . . . , un}...

5 be an n x m matrix and let C A be the set of columns of A Define all anl a12 00 0 an2 alm anm CR rank A dim Span C Now let V W be finite dimensional vector spaces and TV W a linear map between them...

Explain the following que.stions as attached below. Pages 2-5 Q1 a) Let V be a finite dimensional vector space over a field F. If S and S' are two different bases of V, then prove that the number of...

You just need to answer e), but please well-written, Thank you! 8. Let V be a finite dimensional inner product space and let P :V + V be a linear map satisfying p2 = P. (a) Prove that the only...

An experiment was conducted at the University of North Carolina to see whether the biochemical oxygen demand (BOD) test for water pollution is biased by the presence of copper. In this test, the...

Let X be a finite-dimensional normed linear space, and {x1; x2,..., xn} any basis for X. The function f: n X defined by is a linear homeomorphism (remark 2.12). That is, ¢ f is linear ¢ f...

Conditional expectations. Let $(X, \mathscr{A}, \mu)$ be a $\sigma$-finite measure space and $\mathscr{F} \subset \mathscr{A}$ be a sub$\sigma$-algebra. Then use the Radon-Nikodm theorem to...

Prove the following, which is a more general form of Markovs inequality than the one given in Proposition 4.11. Let X be a random variable that takes nonnegative values and for which E(Xk) exists for...

Harper, Inc, acquires 40 percent of the outstanding voting stock of Kinman Company on January 1, 2017, for $210,000 in cash. The net assets on that date was $400,000, although one of the company's...

Excel File Edit View Insert Format Tools Data Window Help 11 8 ) 75% Tue 10:23 AM QE AutoSave OFF A F ? C ... SMS310 Test 2 - Student File Final Home Insert Draw Page Layout Formulas Data Review View...

A developer filed a breach of contract action against a general contractor in federal district court. If the contract was breached, the general contractor believes the fault was that of the framing...

What would be the approximate current flow in a 120 volt circuit with a 400 watt toaster and an 800 watt microwave oven attached

n Suppose X1,..., X are n iid random variables from the cumulative distribution func- tion F(x). Let Y = X; for i = 1,..., n. We further know that X; and Y; have the same distribution. For 0.5

The following was posted 7:09 AM, MAY 4, 2020, by Fox Television Stations, updated AT 07:16AM, May 4, 2020. LITTLE ROCK, Ark. Walmart paid almost $180 million in cash bonuses to its hourly associates...

Problem 8-11A Notes receivable LO4 CHECK FIGURES: d. Interest income =$454.93; e. Cash =$90,499.32 Vauxall Holdings showed the following information regarding its notes receivable: Required For each...

7. FALSE DILEMMA 8. GANDWAGON Definition: Fallacy example: How to revise argument: Definition: Fallacy example: How to revise argument:

Show that (z, w) = wHz defines an inner product on Cn.

An m n matrix A is said to have a right inverse if there exists an n x m matrix C such that AC = Im. A is said to have a left inverse if there exists an n m matrix D such that DA = In. (a) If A has...

Let x and y be vectors in Rn, n > 1. Show that if A = xyT then det(A) = 0.

This problem uses the data from Problem 15 in Chapter 5. a. Using a computer program, fit a cubic polynomial model with BLOODTOL as the response and PPM_TOLU as the predictor. Center PPM_TOLU....

a.-c. Repeat parts (a) through (c) of Problem 1 using the data of Problems 3 through 14 of Chapter 5.

In 1990, Business Week magazine compiled financial data on the 1,000 companies that had the biggest impact on the U.S. economy. Data from this compilation were presented in Problem 13 of Chapter 8....