f(x)=[lnx]

2

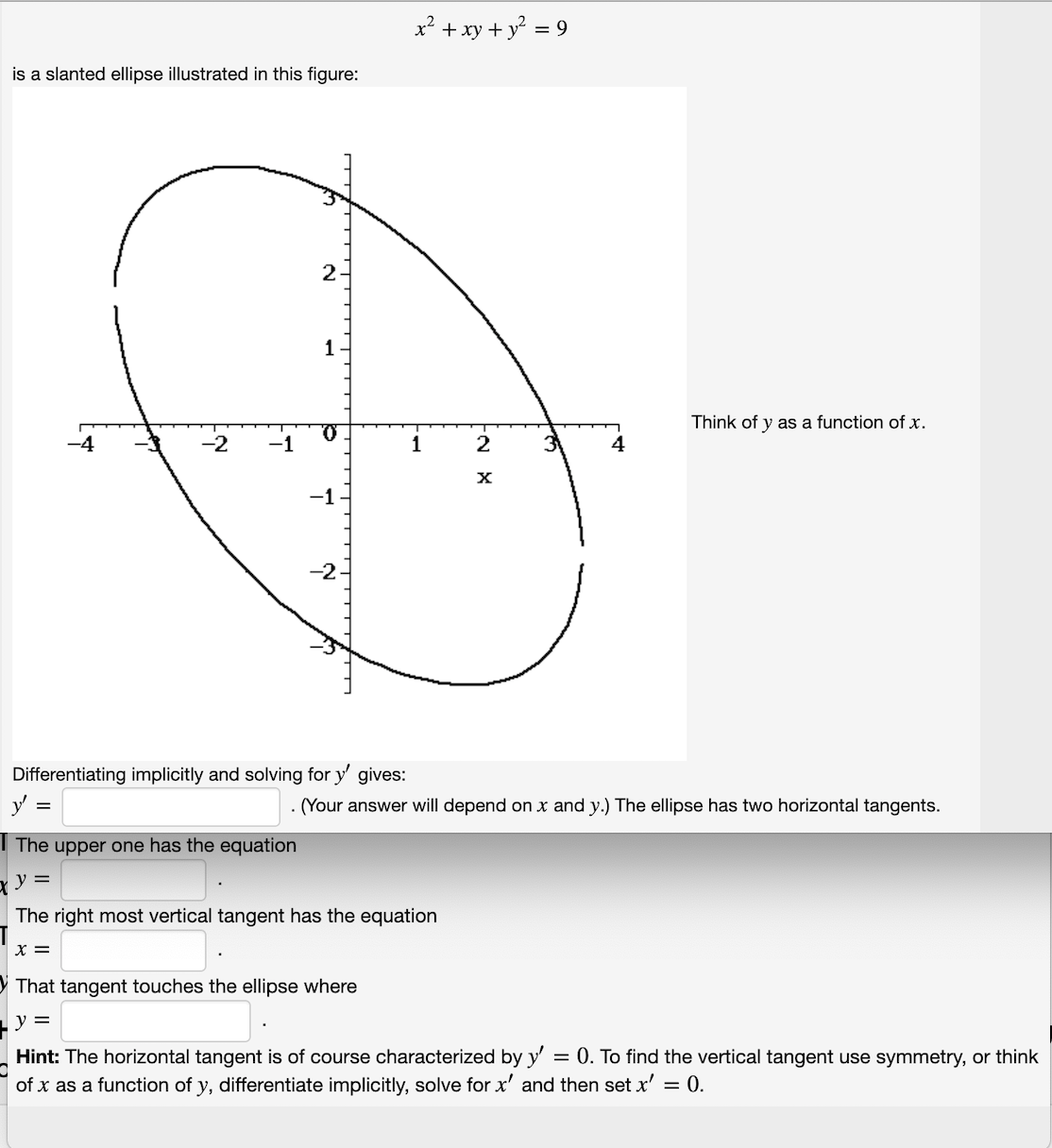
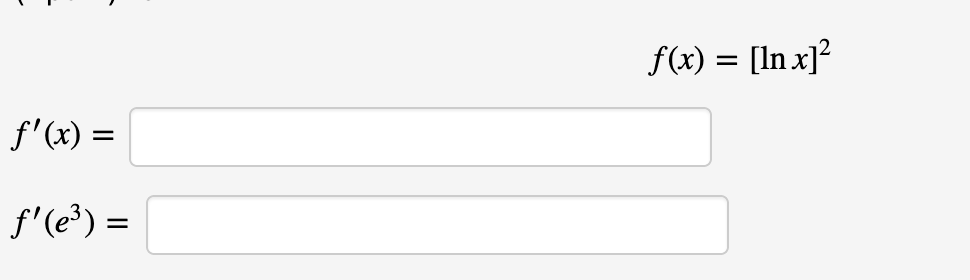
(1 point) Find dy/dx in terms of x and y if cos(2y) + sin (2y) = y + 9. dy dx =(1 point) Find the slope of the tangent line to the curve (a lemniscate) 2(ch2 + 372)2 = 25(x2 y2) at the point (3, 1). m: +w+f=9 is a slanted ellipse illustrated in this gure: Think of y as a function of x. Differentiating implicitly and solving for 3\" gives: y' = . (Your answer will depend on x and y.) The ellipse has two horizontal tangents. =- The right most vertical tangent has the equation That tangent touches the ellipse where Hint: The horizontal tangent is of course characterized by y' = 0. To nd the vertical tangent use symmetry, or think ofx as a function of y, differentiate implicitly, solve for x' and then set x' = 0. (1 point) For the equation given below, evaluate y' at the point (1, 1). 3ety - 5x = y+2.15. y' at (1, 1) =\f