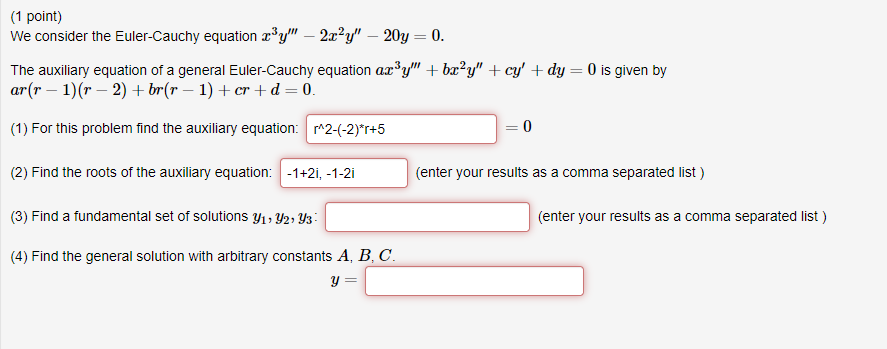
\f(1 point) We consider the Euler-Cauchy equation x y"" -2xly" - 20y = 0. The auxiliary equation of a general Euler-Cauchy equation ar y" + box?y" + cy' + dy = 0 is given by ar(r - 1)(r -2) +br(r - 1) + cr +d =0. (1) For this problem find the auxiliary equation: r 2-(-2)*r+5 0 (2) Find the roots of the auxiliary equation: -1+2i, -1-2i (enter your results as a comma separated list ) (3) Find a fundamental set of solutions y1, y2, y3: (enter your results as a comma separated list ) (4) Find the general solution with arbitrary constants A, B, C. y