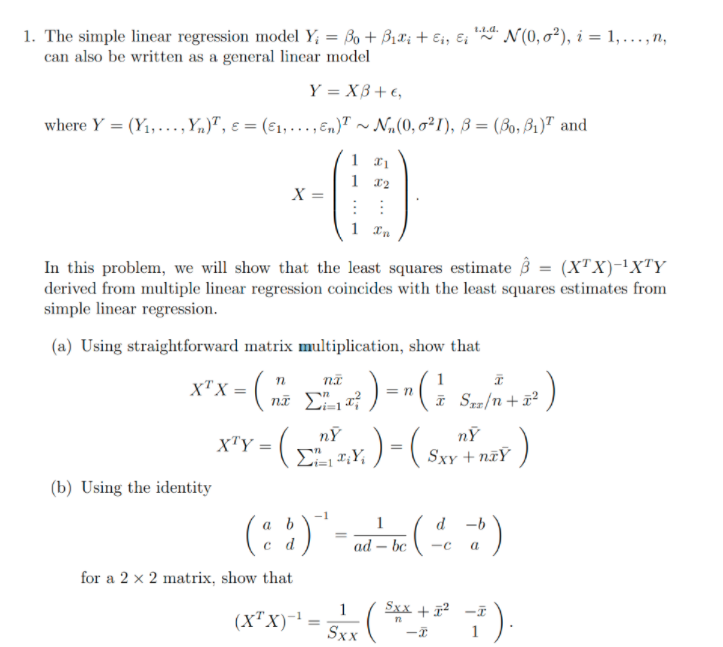
\f1. The simple linear regression model Y, = Bo + Bir; +;, &; " N(0, 0'), i = 1, ..., n, can also be written as a general linear model Y = XB+E, where Y = (Y1, . . ., Yn), E = (61, . . . .E.)? ~ Na. (0, 621), B = (Bo, Bi) and T2 X = In In this problem, we will show that the least squares estimate B = (XTX)-1XTY derived from multiple linear regression coincides with the least squares estimates from simple linear regression. (a) Using straightforward matrix multiplication, show that XX= (ni _mix ) =n( x Smo+2) XTY = _ _X ) =(SxY + niY (b) Using the identity ( " * ) d ad - bc -c a for a 2 x 2 matrix, show that Sxx + 12 (x X)= -I SXX -T 12. Again, consider the general linear model Y = X8 + , with & ~ N,(0, o'/), where the first column of X consists of all ones. (a) Using facts about the mean and variance/covariance of random vectors given in lecture, show that the least squares estimate from multiple linear regression satisfies E(B) = 8 and Var(B) = ?(XTX)-1. (b) Let H = X(X X)-1XT be the hat matrix, Y = HY be the fitted values and e= (I - H)Y be residuals. Using properties derived in class, show that Can = 0. i=1 This fact is used to provide the ANOVA decomposition SSTO = SSE + SSR for multiple linear regression. (Hint: The sum above can be written as e Y. Apply properites of H.)\f3. [10 pts] Consider the simple linear regression model yi = 60+81(xi-x) +ci(i= 1,2,..,n), where x= ni=1 xi. From the least-squares criterion S(80,81), find the least-squares estimators of 80 and 1 for this model. Hint: Do not expand the term (xi-x). That is, do not expand nti= 1 yi*(xi-x) as nZi=1 yixi- nZi=1 yi x for easier computations. Also remember what ni=1(xi-x) is. 3. [10 pts] Consider the simple linear regression model yi = Po + Bi(x; - I) + &; (i=1,2,...,n), where I = _, I;. From the least-squares criterion S(Bo, 81), find the least-squares estimators of Bo and B, for this model. n n Hint: Do not expand the term (r; - I). That is, do not expand ) yi(x, - F) as ur - 1= 1 1=1 n it for easier computations. Also remember what E(x - 1) is. i-1 i-11. The aim of this problem is to give you an example of irreducible Markov chain that is null recurrent. Consider a Markov chain with states 0, 1, 2,... whose non-zero transition probabilities are as listed below: Po,1 = 1, Pm,m+1 = m+ 1' Pm,0= m + 1' m = 1. Let To be the first return time to state 0. (a) Compute P(To = n | Xo = 0) for any n 2 1. (b) Show that P(To nP(To = n | Xo = 0).) n=11. Some (More) Math Review a) Let N = 3. Expand out all the terms in this expression: Cov Xi b) Now write out all the terms using the formula from last class for variance of a sum: Var( X:) = _Var(X) + > > Cov(X, X;) i-1 1=1 i-lj=1ifi Verify that (a) and (b) are giving you the same thing. Hint: Cov(X, X) = Var(X). c) Suppose that D is a roulette wheel that takes on the values {1, 2, 3} all with probability 1/3. What is the expected value of this random variable? What about the variance? d) Now suppose that M is another roulette wheel that takes on the values {1, 2,3} all with probability 1/3. Solve for the expected value of 1/M. e) Finally, suppose that D and M are independent. Solve for: E Hint: You do not need to do any new calculations here. Just remember that for independent RVs, E(XY) = E(X)E(Y). f) Does E(D/M) = E(D)/ E(M)