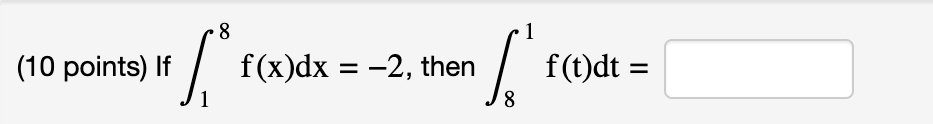
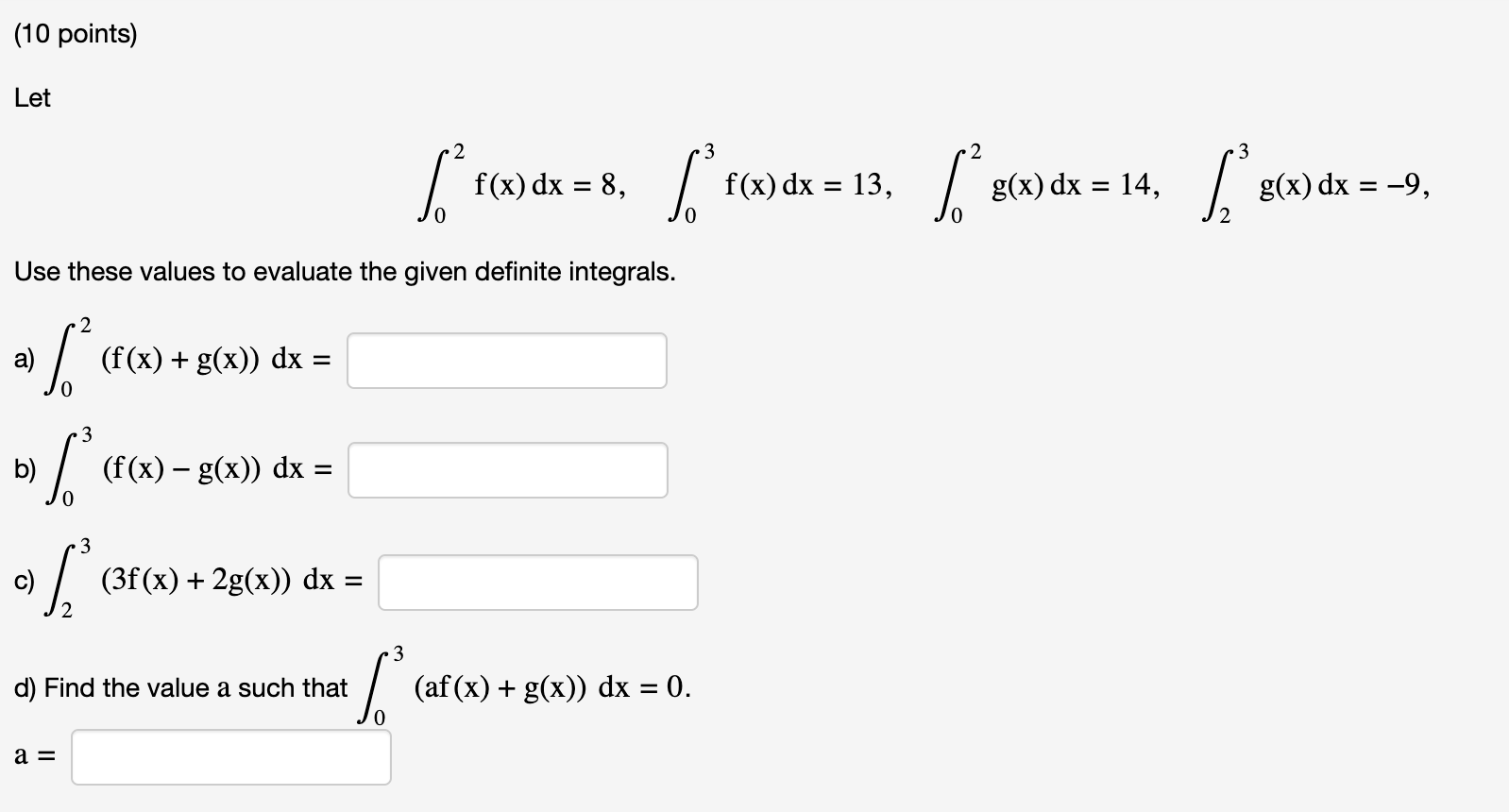
\f(10 points) Let w 2 3 f(x) dx = 8, f(x) dx = 13, o g(x) dx = 14, g(x) dx = -9, Use these values to evaluate the given definite integrals. a) (f (x) + g(x)) dx = b) (f (x) - g(x)) dx = ( 3f (x ) + 2g(x)) dx = d) Find the value a such that (af (x) + g(x)) dx = 0. a =\f(10 points) Let I: f (x) dx = 6. (a) What is the average value of f(x) on the interval from x = 0 to x = 2? average value = (b) If f(x) is even, find each of the following: 2 L2 f(x) dx = the average of f(x) on the interval 1; = 2 to x = 2 = (c) If f(x) is odd, find each of the following: 2 L2 f(x) dx = the average of f(x) on the interval 1; = 2 to x = 2 =