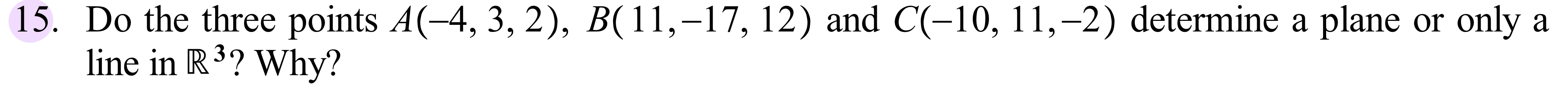
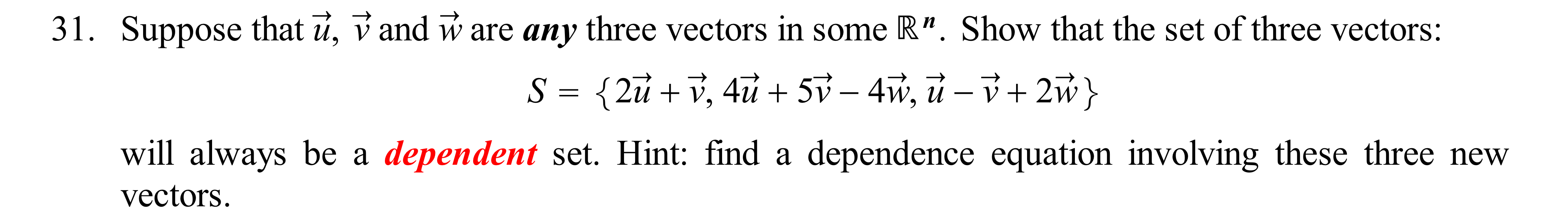
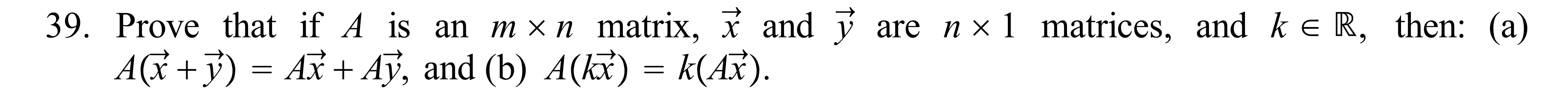
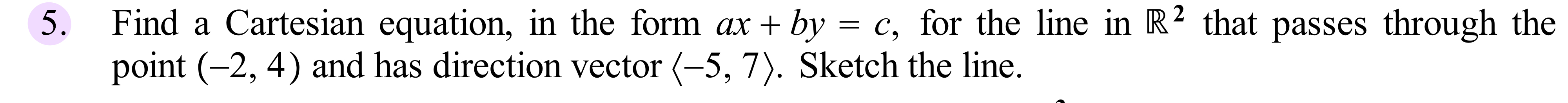
\f15. Do the three points A(4, 3, 2), B(11,17, 12) and C(10,11,2) determine a plane or only a line in R3? Why? 19. Find a Cartesian equation for the plane that contains the line (x, y, z) = (3, 5,4) + t(2, 1, 3) and the point (3,7, 2). For Exercises (25) to (29): The following sets S = {31, 32, ..., T2)\" } C [Rm are all dependent. As before, assemble the vectors as the columns of a matrix A and nd the rref of A. Unlike the sets in Exercises 18 to 24, each associated rref has more than one free variable. Find a dependence equation with the required conditions in each subitem, again with only integer coefcients. 25. S = {(5, 3,6,2>, (3,2, 5, 2}, (1,2, ll, 6), (5,4, l, 6)}. a. Find a dependence equation involving only 72'], T}; and 33. b. Find a dependence equation involving only 31, 72 and 74. c. Find a dependence equation involving only 32, 33 and 34. Hint: use (a) to eliminate 31 from (b). 26. Show algebraically that if if = (ul , L12) and T} = (v1, vz> are vectors in R2 that are not parallel to each other, then any vector (x, y) E R2 can be written as a linear combination of ii and T}. Hint: Use the contrapositive that you wrote in Exercise 19 from Section 1.1. Show that for any x and y, we can solve the vector equation (x, y) = r31 + S? for r and s. You will have to do a Case-byCase Analysis. We suggest the cases: (1) neither ul nor u; is zero, and (2) either ul or Hg is zero (explain why they cannot both be zero). Next, explain why we can further conclude that Span({, 7}) = R2. 27. S = {(5, 3,4,2), (3,2, 4, 2), (1,1, 2, 2),